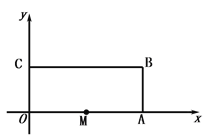
��Ŀ����
����Ŀ����ͼ��������OABC�У�OΪƽ��ֱ������ϵ��ԭ�㣬A�������Ϊ��8��0����C�������Ϊ��0��4������B�ڵ�һ�����ڣ���M��ԭ���������ÿ��2����λ���ȵ��ٶ�����O-A-B-C-O��·���ƶ����˶���O��ֹͣ�˶�����
��1������M�ƶ���5��ʱ����M�������� ��
��2�����ƶ������У���M��y��ľ���Ϊ6����λ����ʱ�����M�ƶ���ʱ���� ��
��3�����ƶ������У���MB=MO�����M�ƶ���ʱ��.
���𰸡���1����8��2������2��3s��7s����3��![]() s��
s��![]() s.
s.
�������������������1����ʱ�估�ٶ������M�˶���·�߳������ݵ�M����O-A-B-C-O��·���ƶ����ɵó���M��λ����
��2���������������������M��OA�ϼ���M��CB��ͨ��ʱ�䣽·�����ٶȼ��ɵó��𰸣�
��3�������������M��OA�ϼ���M��CB�ϣ�Ȼ�����ù��ɶ����������.
�⣺��1����5��2��10����OA��8��
���M�˶���AB���ϣ��Ҿ��A��10-8��2����λ���ȣ�
���M�������ǣ�8��2��.
�ʴ�Ϊ����8��2��.
��2�������������
�ٵ�����OA��ʱ��M��6��0����
��M�˶�·��Ϊ6����λ���ȣ�
���˶�ʱ��Ϊ��6��2��3��s����
�ڵ�����BC��ʱ��M��6��4����
��M�˶�·��Ϊ8+4+2��14����λ���ȣ�
���˶�ʱ��Ϊ��14��2��7��s����
�ʴ�Ϊ��3s��7s.
��3�������������
�ٵ���M��OA��ʱ������BM��

��OM��a,��MB��a��AM��8-a,
��Rt��ABM�У��ɹ��ɶ����ã�
![]() ��
��
���� ![]()
��ã� ![]()
����OM��5��
���Ե�M�˶�ʱ��Ϊ�� ![]() ��s����
��s����
�ڵ���M��BC��ʱ������BO��

ͬ������BM��5��
���Ե�M�˶�ʱ��Ϊ�� ![]() ��s����
��s����
�ʴ�Ϊ�� ![]() s��
s��![]() s.
s.

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�