题目内容
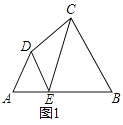
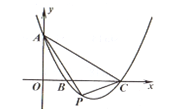
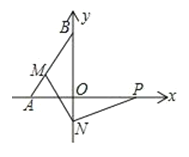
【题目】如图 ，A(－3，0)、B(0，4)、P(4，0)，AB＝5，M、N两点分别在线段 AB、y轴上，则 PN＋MN的最小值为（ ）
A.4B.
C.
D.5
【答案】B
【解析】
如图，连接PN，作NM⊥AB于M，作PM′⊥AB于M′交y轴于点N′．根据垂线段最短可知，PN＋MN的最小值为线段PM′的长，再证明△ABO∽△APM′，可得
，由此即可解决问题；
解：如图，连接PN，作NM⊥AB于M，作PM′⊥AB于M′交y轴于点N′．
∵PN＋MN≥PN′＋N′M′，
即PN＋MN≥PM′，
根据垂线段最短可知，PN＋MN的最小值为线段PM′的长，
∵∠BAO＝∠PAM′，∠AOB＝∠AM′P＝90°，
∴△ABO∽△APM′，
∴，
∴
，
∴PM′＝
∴PN＋MN的最小值为，
故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】七（1）班同学为了解2017年某小区家庭月均用水情况，随机调查了该小区的部分家庭，并将调查数据进行如下整理.请解答以下问题：
月均用水量 | 频数（户数） | 百分比 |
| 6 |
|
|
| |
| 16 |
|
| 10 |
|
| 4 | |
| 2 |
|
（1）请将下列频数分布表和频数分布直方图补充完整；
（2）求该小区月均用水量不超过
的家庭占被调查家庭总数的百分比；
（3）若该小区有1000户家庭，根据调查数据估计该小区月均用水量超过
的家庭数.
【题目】下表是某校七﹣九年级某月课外兴趣小组活动时间统计表，其中各年级同一兴趣小组每次活动时间相同，但表格中九年级的两个数据被遮盖了，记得九年级文艺小组活动次数与科技小组活动次数相同．
年级 | 课外小组活动总时间（单位：h） | 文艺小组活动次数 | 科技小组活动次数 |
七年级 | 17 | 6 | 8 |
八年级 | 14.5 | 5 | 7 |
九年级 | 12.5 |
|
|
则九年级科技小组活动的次数是_____．
