题目内容
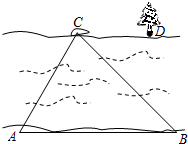
如图,为了测量河宽,在河的一边沿岸选取A、B两点,对岸岸边有一块石头C.在△ABC中,测得∠A=60°,∠B=45°,AB=60米.
(1)求河宽(用精确值表示,保留根号);
(2)如果对岸岸边有一棵大树D,且CD∥AB,并测得∠DAB=37°,求C、D两点之间的距离(结果精确到0.1米).(参考数据:
≈1.41,
≈1.73,sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,cot37°≈1.33)
(1)求河宽(用精确值表示,保留根号);
(2)如果对岸岸边有一棵大树D,且CD∥AB,并测得∠DAB=37°,求C、D两点之间的距离(结果精确到0.1米).(参考数据:
| 2 |
| 3 |

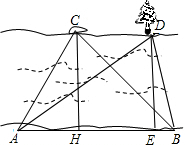
(1)过点C作CH⊥AB,垂足为点H,河宽就是CH的长.
在△ACH中,cotA=
,得AH=CH•cotA.
同理可得BH=CH•cotB.
∵AH+BH=AB,
∴CH•cot60°+CH•cot45°=60.
∴CH=
=90-30
(米);
(2)过点D作DE⊥AB,垂足为点E.
在△ADE中,cot∠DAE=
=
.
∴AE=(90-30
)•cot37°≈50.67.
同理可得AH≈21.96.
∴CD=HE=50.67-21.96=28.71≈28.7(米).
答:河宽等于(90-30
)米,C、D两点之间的距离约等于28.7米.
在△ACH中,cotA=
| AH |
| CH |
同理可得BH=CH•cotB.
∵AH+BH=AB,
∴CH•cot60°+CH•cot45°=60.
∴CH=
| 60 | ||||
|
| 3 |
(2)过点D作DE⊥AB,垂足为点E.
在△ADE中,cot∠DAE=
| AE |
| DE |
| AE |
| CH |
∴AE=(90-30
| 3 |
同理可得AH≈21.96.
∴CD=HE=50.67-21.96=28.71≈28.7(米).
答:河宽等于(90-30
| 3 |


练习册系列答案
相关题目
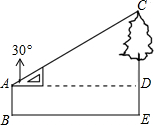
 影响.
影响.
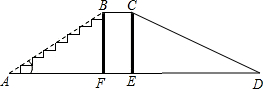 F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=
F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=