题目内容
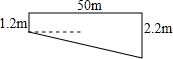
某公园有一滑梯,横截面如图所示,AB表示楼梯,BC表示平台,CD表示滑道.若点E,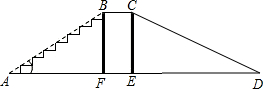 F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=
F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=
,BF=3米,BC=1米,CD=6米.
求:(1)∠D的度数;
(2)线段AE的长.
 F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=
F均在线段AD上,四边形BCEF是矩形,且sin∠BAF=| 2 |
| 3 |
求:(1)∠D的度数;
(2)线段AE的长.
(1)Rt△CED中,CE=BF=3米,CD=6米,
∴sinD=
=
,
∴∠D=30°;
(2)Rt△ABF中,sin∠BAF=
,BF=3米,
∴AB=BF÷sin∠BAF=3÷
=4.5米.
由勾股定理,得:AF=
=
米,
∴AE=AF+EF=AF+BC=(
+1)米.
∴sinD=
| CE |
| CD |
| 1 |
| 2 |
∴∠D=30°;
(2)Rt△ABF中,sin∠BAF=
| 2 |
| 3 |
∴AB=BF÷sin∠BAF=3÷
| 2 |
| 3 |
由勾股定理,得:AF=
| AB2-BF2 |
3
| ||
| 2 |
∴AE=AF+EF=AF+BC=(
3
| ||
| 2 |

练习册系列答案
相关题目