题目内容

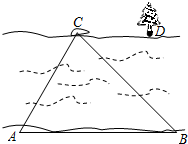
如图，一学生要测量校园内一颗水杉树的高度，他站在距离水杉树10m的B处，测得树顶的仰角为∠CAD=30°，已知测角仪的架高AB=2m，那么这棵水杉树高是（　　）
A．（
10
3
3
+2）m		B．（10+2）mC．
10
3
3
m		D．7m

过A作AD⊥CE于D，
则四边形ABDE为矩形，
可得：AD=BE=10m，AB=DE=2m，
在Rt△ACD中，
∵∠CAD=30°，AD=10m，
∴
CD
AD
=tan∠CAD=tan30°，
∴CD=AD×
3
3
=
10
3
3
（m），
则树高CE=CD+DE=（
10
3
2
+2）m．
故选A．
练习册系列答案
相关题目
花园小区有一朝向为正南方向的居民楼（如图），该居民楼的一楼是高4米的小区商场，商场以上是居民住房．在该楼的前面16米处要盖一栋高18米的办公楼．当冬季正午的阳光与水平线的夹角为35°时，问：
（1）商场以上的居民住房采光是否有影响，为什么？
（2）若要使商场采光不受影响，两楼应相距多少米？（结果保留一位小数）
（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）
2009年3月29日，宁波市第二届山地户外运动挑战赛在奉化市大堰镇举行，比赛全程42公里，共有20支队伍参加，其中三支外国队．划皮艇横渡柏坑水库是其中一个项目，横渡直线距离900米．在实际比赛中，甲队皮艇的划行路线偏离了最短路线约5°，但甲队还是以15分钟12秒的成绩摘得冠军．问：
（1）在这次比赛中，甲队皮艇的平均速度为多少？（精确到0.01米/秒）
（2）若甲队划皮艇的平均速度不变且在比赛中沿最短路线划行，则可比实际比赛提前几秒到达终点？（精确到0.1秒）
（参考数据：sin5°=0.0872；cos5°=0.9962；tan5°=0.0875）
如图，为了测量河宽，在河的一边沿岸选取A、B两点，对岸岸边有一块石头C．在△ABC中，测得∠A=60°，∠B=45°，AB=60米．
（1）求河宽（用精确值表示，保留根号）；
（2）如果对岸岸边有一棵大树D，且CD∥AB，并测得∠DAB=37°，求C、D两点之间的距离（结果精确到0.1米）．（参考数据：
2
≈1.41，
3
≈1.73，sin37°≈0.60，cos37°≈0.80，tan37°≈0.75，cot37°≈1.33）
下列说法正确的是（　　）
A．三角形的重心是三角形三边垂直平分线的交点
B．三角形的一条中位线与第三边上的中线互相平分
C．坡面的水平长度l与铅垂高度h的比是坡比i=
l
h
D．相似三角形对应高的比等于相似比的平方
如图，两条宽度均为a的公路相交成α角，这两条公路在相交处的公共部分的面积是（　　）
A．
a2
sinα
B．
a2
cosα
C．a2sinαD．a2cosα
Given△ABC with∠ACB=90°，∠ABC=15°，AC=1，thenthelengthofBCis（　　）
A．2+
3
B．3+
2
C．3-
2
D．
2
+
3
如图，一艘货轮向正北方向航行，在点A处测得灯塔M在北偏西30°，货轮以每小时20海里的速度航行，1小时后到达B处，测得灯塔M在北偏西45°，问该货轮到达灯塔正东方向D处时，货轮与灯塔M的距离是多少？
（精确到0.1海里，
3
≈1.732）
如图，某数学兴趣小组在活动课上测量学校旗杆高度．已知小明的眼睛与地面的距离（AB）是1.7m，看旗杆顶部M的仰角为45°；小红的眼睛与地面的距离（CD）是1.5m，看旗杆顶部M的仰角为30°．两人相距30米且位于旗杆两侧（点B，N，D在同一条直线上）．求旗杆MN的高度．（参考数据：
2
≈1.4，
3
≈1.7，结果保留整数）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网