题目内容
【题目】已知二次函数y=x2+bx+c的图象经过(0,3),(4,3).
(1)求b、c的值.
(2)开口方向 ,对称轴为 ,顶点坐标为 .
(3)该函数的图象怎样由y=x2的图象平移得到.
【答案】(1)b=-4,c=3;(2)向上,直线x=2,(2,﹣1);(3)y=(x﹣2)2﹣1是由y=x2向右平移2个单位,向下平移1个单位得到的.
【解析】
(1)将(0,3)(4,3)两点坐标代入y=x2+bx+c,解方程即可求得b、c的值;
(2)根据二次函数的性质,利用配方法求出求出函数的最值与对称轴即可;
(3)根据平移规律直接回答即可.
解:(1)由于二次函数y=x2+bx+c的图象经过点(0,3)、(4,3),
则![]() ,解得:
,解得:![]() ;
;
(2)由二次函数y=x2﹣4x+3可知:a=1,开口方向向下;
原二次函数经变形得:y=(x﹣2)2﹣1,
故顶点为(2,﹣1),对称轴是直线x=2
故答案为向上,直线x=2,(2,﹣1);
(3)y=(x﹣2)2﹣1是由y=x2向右平移2个单位,向下平移1个单位得到的.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
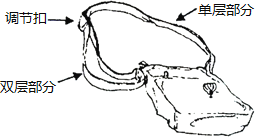
【题目】如图,是一种斜挎包,其挎带由双层部分、单层部分和调节扣构成.小垣用后发现,通过调节扣加长或缩短单层部分的长度,可以使挎带的长度(单层部分与双层部分长度的和,其中调节扣所占的长度忽略不计)加长或缩短.设单层部分的长度为xcm,双层部分的长度为ycm,经测量,得到如下数据:
(1)根据表中数据的规律,补全以下表格,并求出y关于x的函数表达式;
单层部分的长度x(cm) | … | 4 | 6 | 8 | 10 | … | 150 |
双层部分的长度y(cm) | … | 73 | 72 | 71 | ______ | … | ______ |
(2)根据小垣的身高和习惯,挎带的长度为120cm时,背起来正合适,请求出此时单层部分的长度.