��Ŀ����
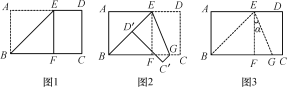
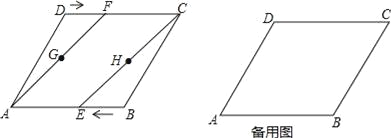
����Ŀ����ͼ��������ABCD�У�AB=4cm����BAD=60�㣮����E��F�ֱ�ӵ�B��Dͬʱ��������1cm/s���ٶ����A��C�˶�������AF��CE��ȡAF��CE���е�G��H������GE��FH�����˶���ʱ��Ϊts��0��t��4����
��1����֤��AF��CE��
��2����tΪ��ֵʱ���ı���EHFGΪ���Σ�
��3����̽�����Ƿ����ij��ʱ��t��ʹ�ı���EHFGΪ���Σ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��֤������������2��t=1����3��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�
��������
��1���������ε����ʵõ���B=��D��AD=BC��AB��DC���Ƴ���ADF�ա�CBE������ȫ�������ε����ʵõ���DFA=��BEC������ƽ���ߵ��ж��������ɵõ����ۣ�
��2����D��DM��AB��M������GH��EF���Ƴ��ı���AECF��ƽ���ı��Σ��������ε��ж��������ɵõ��ı���EGFH�����Σ�֤���ı���DMEF�Ǿ��Σ����ǵõ�ME=DF=t�з��̼��ɵõ����ۣ�
��3�������ڣ��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ����ݾ��ε������з��̼��ɵõ������
��1��֤�����߶���E��Fͬʱ�˶����ٶ���ȣ�
��DF=BE��
���ı���ABCD�����Σ�
���B=��D��AD=BC��AB��DC��
����ADF����CBE��
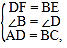
���ADF�ա�CBE��
���DFA=��BEC��
��AB��DC��
���DFA=��FAB��
���FAB=��BEC��
��AF��CE��
��2����D��DM��AB��M������GH��EF��
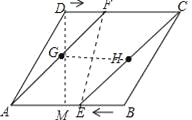
��DF=BE=t��
��AF��CE��AB��CD��
���ı���AECF��ƽ���ı��Σ�
��G��H��AF��CE���е㣬
��GH��AB��
���ı���EGFH�����Σ�
��GH��EF��
��EF��AB����FEM=90�㣬
��DM��AB��
��DM��EF��
���ı���DMEF�Ǿ��Σ�
��ME=DF=t��
��AD=4����DAB=60�㣬DM��AB��
��![]()
��BE=4��2��t=t��
��t=1��
��3�������ڣ��������ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�
���ı���EHFGΪ���Σ�
��EF=GH��
��EF2=GH2��
��![]() ���t=0��0��t��4��
���t=0��0��t��4��
����ԭ����ì�ܣ�
�����ij��ʱ��t��ʹ�ı���EHFGΪ���Σ�

 ��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д�
��У��ʦ������ҵ���Ӻ����Ծ�ϵ�д� ȫ�̽��ϵ�д�
ȫ�̽��ϵ�д�����Ŀ���üס�������ԭ�����Ƴ�ij�����ϣ���֪������ԭ�ϵ�ά���غ���C����������ԭ�ϵļ۸����±�:
�� | �� | |
ά����C����λ/ǧ�ˣ� | 600 | 100 |
ԭ�ϼ۸�Ԫ/ǧ�ˣ� | 8 | 4 |
��������������10ǧ�ˣ�Ҫ�����ٺ���4200��λ��ά����C����Ҫ����ס�������ԭ�ϵķ��ò�����72Ԫ.���ʣ���Ҫ����Ҫ����Ҫ�ɱ���ͣ��������ԭ��Ӧ����ʲô��Χ֮�ڣ���ͳɱ��Ƕ���Ԫ��