题目内容
【题目】已知反比例函数y＝
的图象与一次函数y＝ax+b的图象交于点A（1，4）和点B（m，﹣2），
（1）求这两个函数的关系式；
（2）观察图象，写出使得＞ax+b成立的自变量x的取值范围；
（3）过点A作AC⊥x轴，垂足为C，在平面内有点D，使得以A，O，C，D四点为顶点的四边形为平行四边形，直接写出符合条件的所有D点的坐标．
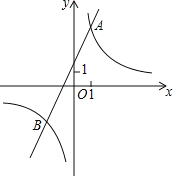
【答案】（1）y＝2x+2；（2）x＜﹣2或0＜x＜1；（3）（0，﹣4），（0，4）或（2，4）．
【解析】
（1）首先将A点坐标代入反比例函数，进而计算出k的值，再将B点代入反比例函数的关系式，求得参数m的值，再利用待定系数法求解一次函数的解析式.
（2）根据题意要使
＞ax+b则必须反比例函数的图象在一次函数之上，观察图象即可得到x的取值范围.
（3）首先写出A、C的坐标，再根据对角为OC、OA、AC进行分类讨论.
解：（1）将A（1，4）代入y＝，得：4＝k，
∴反比例函数的关系式为y＝
；
当y＝﹣2时，﹣2＝
，解得：m＝﹣2，
∴点B的坐标为（﹣2，﹣2）．
将A（1，4），B（﹣2，﹣2）代入y＝ax+b，得：
，
解得：
，
∴一次函数的关系式为y＝2x+2．
（2）观察函数图象，可知：当x＜﹣2或0＜x＜1时，反比例函数图象在一次函数图象上方，
∴使得＞ax+b成立的自变量x的取值范围为x＜﹣2或0＜x＜1．
（3）∵点A的坐标为（1，4），
∴点C的坐标为（1，0）．
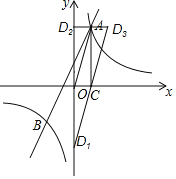
设点D的坐标为（c，d），分三种情况考虑，如图所示：
①当OC为对角线时，
，
解得：
，
∴点D1的坐标为（0，﹣4）；
②当OA为对角线时，
解得： 
∴点D2的坐标为（0，4）；
③当AC为对角线时，
，
解得：
，
∴点D3的坐标为（2，4）．
综上所述：以A，O，C，D四点为顶点的四边形为平行四边形时，点D的坐标为（0，﹣4），（0，4）或（2，4）．
