题目内容
【题目】在学完“有理数的运算”后，某中学七年级各班各选出5名学生组成一个代表队，在数学方老师的组织下进行一次知识竞赛，竞赛规则是:每队都分别给出50道题，答对一题得3分，不答或答错一题倒扣1分
（1）如果2班代表队最后得分142分，那么2班代表队回答对了多少道题？
（2）1班代表队的最后得分能为145分吗？请简要说明理由.
【答案】（1）48（2）不能
【解析】
（1）如果设答对x道题，那么得分为3x分，扣分为（50-x）分．根据具体的等量关系即可列出方程求解；
（2）设答对x道题，根据题意列出方程，若有整数解则能，否则不能．
（1）设2班代表队答对了x道题，
根据题意列方程：3x-（50-x）=142，
解这个方程得：x=48．
故2班代表队答对了48道题；
（2）设1班代表队答对了x道题，
根据题意列方程“3x-（50-x）=145，
解这个方程得：x＝48
．
因为题目个数必须是自然数，
即x＝48不符合该题的实际意义，
所以此题无解．
即1班代表队的最后得分不可能为145分．
黄冈小状元解决问题天天练系列答案
三点一测快乐周计划系列答案
【题目】国务院办公厅2015年3月16日发布了《中国足球改革的总体方案》，这是中国足球历史上的重大改革．为了进一步普及足球知识，传播足球文化，我市举行了“足球进校园”知识竞赛活动，为了解足球知识的普及情况，随机抽取了部分获奖情况进行整理，得到下列不完整的统计图表：
获奖等次 | 频数 | 频率 |
一等奖 | 10 | 0.05 |
二等奖 | 20 | 0.10 |
三等奖 | 30 | b |
优胜奖 | a | 0.30 |
鼓励奖 | 80 | 0.40 |
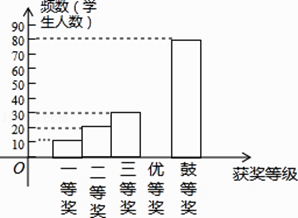
请根据所给信息，解答下列问题：
（1）a= ， b= ， 且补全频数分布直方图；
（2）若用扇形统计图来描述获奖分布情况，问获得优胜奖对应的扇形圆心角的度数是多少？
（3）在这次竞赛中，甲、乙、丙、丁四位同学都获得一等奖，若从这四位同学中随机选取两位同学代表我市参加上一级竞赛，请用树状图或列表的方法，计算恰好选中甲、乙二人的概率．
