Question

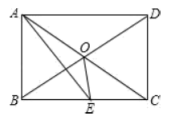
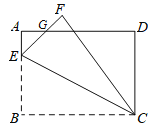
【题目】如图，矩形ABCD中，AB=4，BC=6，E为AB上一点，将△BCE沿CE翻折至△FCE，EF与AD相交于点G，且AG=FG，则线段AE的长为__________．

Answer 1

【答案】1

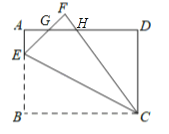
【解析】解：如图所示．∵四边形ABCD是矩形，∴∠D=∠B=∠A=90°，AB=CD=4，AD=BC=6，根据题意得：△BCE≌△CEF，∴EF=BE，∠F=∠B=90°，CF=BC=6．在△GAE和△GFH中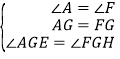，，∴△GAE≌△GFH（ASA），∴EG=GH，AE=FH，∴AH=EF，设BE=EF=x，则AE=FH=4﹣x，AH=x，∴DH=6﹣x，CH=6﹣（4﹣x）=2+x，根据勾股定理得：DC2+DH2=CH2，即42+（6﹣x）2=（x+2）2，解得：x=3，∴BE=3，∴AE=1．故答案为：1．