ЬтФПФкШн
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌЙцЖЈЃКХзЮяЯпy=aЃЈxЉhЃЉ2+kЕФЙиСЊжБЯпЮЊy=aЃЈxЉhЃЉ+kЃЎ
Р§ШчЃКХзЮяЯпy=2ЃЈx+1ЃЉ2Љ3ЕФЙиСЊжБЯпЮЊy=2ЃЈx+1ЃЉЉ3ЃЌМДy=2xЉ1ЃЎ
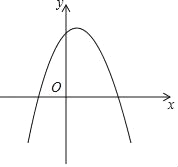
ЃЈ1ЃЉШчЭМЃЌЖдгкХзЮяЯпy=ЉЃЈxЉ1ЃЉ2+3ЃЎ
ЂйИУХзЮяЯпЕФЖЅЕузјБъЮЊ_____ЃЌЙиСЊжБЯпЮЊ_____ЃЌИУХзЮяЯпгыЦфЙиСЊжБЯпЕФНЛЕузјБъЮЊ_____КЭ_____ЃЛ
ЂкЕуPЪЧХзЮяЯпy=ЉЃЈxЉ1ЃЉ2+3ЩЯвЛЕуЃЌЙ§ЕуPЕФжБЯпPQДЙжБгкxжсЃЌНЛХзЮяЯпy=ЉЃЈxЉ1ЃЉ2+3ЕФЙиСЊжБЯпгкЕуQЃЎЩшЕуPЕФКсзјБъЮЊmЃЌЯпЖЮPQЕФГЄЖШЮЊdЃЈdЃО0ЃЉЃЌЧѓЕБdЫцmЕФдіДѓЖјМѕаЁЪБЃЌdгыmжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПmЕФШЁжЕЗЖЮЇЃЎ
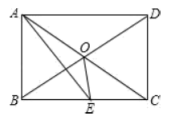
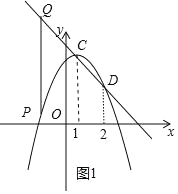
ЃЈ2ЃЉЖЅЕудкЕквЛЯѓЯоЕФХзЮяЯпy=ЉaЃЈxЉ1ЃЉ2+4aгыЦфЙиСЊжБЯпНЛгкЕуAЃЌBЃЈЕуAдкЕуBЕФзѓВрЃЉЃЌгыxжсИКАыжсНЛгкЕуCЃЌжБЯпABгыxжсНЛгкЕуDЃЌСЌНсACЁЂBCЃЎ
ЂйЧѓЁїBCDЕФУцЛ§ЃЈгУКЌaЕФДњЪ§ЪНБэЪОЃЉЃЎ
ЂкЕБЁїABCЮЊЖлНЧШ§НЧаЮЪБЃЌжБНгаДГіaЕФШЁжЕЗЖЮЇЃЎ
ЁОД№АИЁП ЃЈ1ЃЌ3ЃЉ y=Љx+4 ЃЈ1ЃЌ3ЃЉ ЃЈ2ЃЌ2ЃЉ
ЁОНтЮіЁПЪдЬтЗжЮіЃК ![]() ЂйжБНгаДГіХзЮяЯпЕФЖЅЕузјБъЃЌИљОнЙиСЊжБЯпЕФЖЈвхЧѓГіЙиСЊжБЯпЕФЗНГЬЃЌСЊСЂЗНГЬМДПЩЧѓГіЫќУЧЕФНЛЕузјБъ.
ЂйжБНгаДГіХзЮяЯпЕФЖЅЕузјБъЃЌИљОнЙиСЊжБЯпЕФЖЈвхЧѓГіЙиСЊжБЯпЕФЗНГЬЃЌСЊСЂЗНГЬМДПЩЧѓГіЫќУЧЕФНЛЕузјБъ.
ЂкЩш![]() дђ
дђ![]() вђЮЊdЫцmЕФдіДѓЖјМѕаЁЃЌЕУГі
вђЮЊdЫцmЕФдіДѓЖјМѕаЁЃЌЕУГі![]() Лђ
Лђ![]() ЗжСНжжЧщПіНјааЬжТл.
ЗжСНжжЧщПіНјааЬжТл.
![]() ЂйИљОнЙиСЊжБЯпЕФЖЈвхЧѓГіЙиСЊжБЯпЕФЗНГЬЃЌСЊСЂЗНГЬМДПЩЧѓГіЫќУЧЕФНЛЕу
ЂйИљОнЙиСЊжБЯпЕФЖЈвхЧѓГіЙиСЊжБЯпЕФЗНГЬЃЌСЊСЂЗНГЬМДПЩЧѓГіЫќУЧЕФНЛЕу![]() ЕФзјБъ.ЧѓГі
ЕФзјБъ.ЧѓГі![]() СНЕуЕФзјБъЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪННјааЧѓНтМДПЩ.
СНЕуЕФзјБъЃЌИљОнШ§НЧаЮЕФУцЛ§ЙЋЪННјааЧѓНтМДПЩ.
Ђк![]() ЗжСНжжЧщПіНјааЬжТлМДПЩ.
ЗжСНжжЧщПіНјааЬжТлМДПЩ.
ЪдЬтНтЮіЃКЃЈ1ЃЉЂйХзЮяЯпЕФЖЅЕузјБъЮЊ![]() ,ЙиСЊжБЯпЮЊ
,ЙиСЊжБЯпЮЊ![]()
НтЗНГЬзщ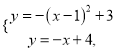 ЕУ
ЕУ![]() Лђ
Лђ![]()
ЫљвдИУХзЮяЯпгыЦфЙиСЊжБЯпЕФНЛЕузјБъЮЊ![]() КЭ
КЭ![]()
ЙЪД№АИЮЊЃК ![]() ЃЌ
ЃЌ ![]()
![]() КЭ
КЭ![]()
ЂкЩш![]() дђ
дђ![]()
ШчЭМ1ЃЌ
ЁпdЫцmЕФдіДѓЖјМѕаЁЃЌ
Ёр![]() Лђ
Лђ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]()
ЕБ![]() ЃЌdЫцmЕФдіДѓЖјМѕаЁЃЌ
ЃЌdЫцmЕФдіДѓЖјМѕаЁЃЌ
злЩЯЫљЪіЃЌЕБ![]() ЃЌ
ЃЌ ![]()
![]() ЪБЃЌ
ЪБЃЌ ![]()
ЃЈ2ЃЉЂйХзЮяЯп![]() ЕФЖЅЕузјБъЮЊЃК
ЕФЖЅЕузјБъЮЊЃК ![]() дкЕквЛЯѓЯоЃЌдђ
дкЕквЛЯѓЯоЃЌдђ![]()
ХзЮяЯп![]() ЕФЙиСЊжБЯпЮЊ
ЕФЙиСЊжБЯпЮЊ![]()
НтЗНГЬзщ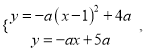 ЕУ
ЕУ![]() Лђ
Лђ![]()
Ёр![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() НтЕУ
НтЕУ![]() дђ
дђ![]()
ЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() НтЕУ
НтЕУ![]() дђ
дђ![]()
Ёр![]()
Ђк![]()
ЕБ![]()
![]() ЮЊЖлНЧЃЌМД
ЮЊЖлНЧЃЌМД![]() НтЕУ
НтЕУ![]()
ЕБ![]()
![]() ЮЊЖлНЧЃЌМД
ЮЊЖлНЧЃЌМД![]() НтЕУ
НтЕУ![]()
злЩЯЫљЪіЃЌaЕФШЁжЕЗЖЮЇЮЊ![]() Лђ
Лђ![]()

 ПЮПЮЭЈПЮГЬБъзМЫМЮЌЗНЗЈгыФмСІбЕСЗЯЕСаД№АИ
ПЮПЮЭЈПЮГЬБъзМЫМЮЌЗНЗЈгыФмСІбЕСЗЯЕСаД№АИЁОЬтФПЁПгЩШєИЩИіБпГЄЮЊ1ЕФаЁе§ЗНаЮзщГЩЕФЭјИёЃЌаЁе§ЗНаЮЕФЖЅЕуНазіИёЕуЃЌвдИёЕуЮЊЖЅЕуЕФЖрБпаЮНаИёЕуЖрБпаЮЃЎЩшИёЕуЖрБпаЮЕФУцЛ§ЮЊSЃЌЫќИїБпЩЯИёЕуЕФИіЪ§КЭЮЊxЃЎ
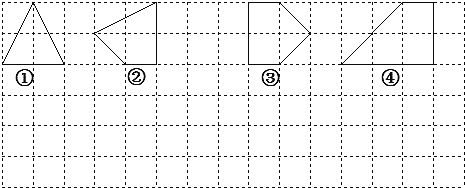
ЃЈ1ЃЉЩЯЭМжаЕФИёЕуЖрБпаЮЃЌЦфФкВПЖМжЛгавЛИіИёЕуЃЌЫќУЧЕФУцЛ§ЃЈSЃЉгыИїБпЩЯИёЕуЕФИіЪ§КЭЃЈxЃЉЕФЖдгІЙиЯЕШчЯТБэЃЌЧыаДГіSгыxжЎМфЕФЙиЯЕЪНЃЎД№ЃКS=_________ЃЎ
ЖрБпаЮЕФађКХ | Ђй | Ђк | Ђл | Ђм | Ё |
ЖрБпаЮЕФУцЛ§S | 2 | 2.5 | 3 | 4 | Ё |
ИїБпЩЯИёЕуЕФИіЪ§КЭx | 4 | 5 | 6 | 8 | Ё |
ЃЈ2ЃЉЧыдйЛГіШ§ИіБпЪ§ЗжБ№ЮЊ3ЁЂ4ЁЂ5ЕФИёЕуЖрБпаЮЃЌЪЙетаЉЖрБпаЮФкВПЖМЪЧгаЧвжЛга2ИіИёЕуЃЎПЩЕУДЫРрЖрБпаЮЕФУцЛ§ЃЈSЃЉгыЫќИїБпЩЯИёЕуЕФИіЪ§КЭЃЈxЃЉжЎМфЕФЙиЯЕЪНЪЧЃКS=________ЃЎ