题目内容
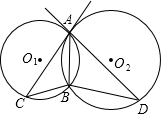
已知等边△ABC边长为a,D、E分别为AB、AC边上的动点,且在运动时保持DE∥BC,如图(1),⊙O1与⊙O2都不在△ABC的外部,且⊙O1、⊙O2分别与∠B和∠C的两边及DE都相切,其中和DE、BC的切点分别为M、N、M′、N′.
(1)求证:⊙O1和⊙O2是等圆;
(2)设⊙O1的半径长为x,圆心距O1O2为y,求y与x的函数关系式,并写出x的取值范围;
(3)当⊙O1与⊙O2外切时,求x的值;
(4)如图(2),当D、E分别是AB、AC边的中点时,将⊙O2先向左平移至和⊙O1重合,然后将重合后的圆沿着△ABC内各边按图(2)中箭头的方向进行滚动,且总是与△ABC的边相切,当点O1第一次回到它原来的位置时,求点O1经过的路线长度?

(1)求证:⊙O1和⊙O2是等圆;
(2)设⊙O1的半径长为x,圆心距O1O2为y,求y与x的函数关系式,并写出x的取值范围;
(3)当⊙O1与⊙O2外切时,求x的值;
(4)如图(2),当D、E分别是AB、AC边的中点时,将⊙O2先向左平移至和⊙O1重合,然后将重合后的圆沿着△ABC内各边按图(2)中箭头的方向进行滚动,且总是与△ABC的边相切,当点O1第一次回到它原来的位置时,求点O1经过的路线长度?

(1)连接MM′、NN′.
∵DE和BC是⊙O1的切线,DE∥BC,
∴MM′过点O1.同理NN'过点O2.∵MM′⊥BC,MM′⊥DE,NN′⊥BC
∴四边形MM′N′N是矩形.
∴MM′=NN′,即⊙O1和⊙O2是等圆;
(2)连接OlB,OlO2,O2C,OlM′,O2N′.
易证四边形O1BCO2是等腰梯形,四边形O1M′N′O2是矩形.
在Rt△O1BM′中,∠01BM′=30°,OlM′=x,
则BM′=
x.
∵y=O102=M′N′,BM′=N′C=
x,BC=BM′+M′N′+N′C,
∴y+2
=a,
∴y=a-2
x,
求得0<x≤
a;
(3)当⊙Ol和⊙O2外切时,OlO2=2x,2x=a-2
x,
∴x=(
-1)
;
(4)当DE是△ABC的中位线时,求得x=
a.
此时BM'=
x=
a.
⊙O1的圆心O1所经过的路线是与△ABC相似,且各边与△ABC各边距离为
a的正三角形.
其边长为a-
a×2=
,
∴所求的圆心O1走过的长度为:
×3=
a.
∵DE和BC是⊙O1的切线,DE∥BC,
∴MM′过点O1.同理NN'过点O2.∵MM′⊥BC,MM′⊥DE,NN′⊥BC

∴四边形MM′N′N是矩形.
∴MM′=NN′,即⊙O1和⊙O2是等圆;
(2)连接OlB,OlO2,O2C,OlM′,O2N′.
易证四边形O1BCO2是等腰梯形,四边形O1M′N′O2是矩形.
在Rt△O1BM′中,∠01BM′=30°,OlM′=x,
则BM′=
| 3 |
∵y=O102=M′N′,BM′=N′C=
| 3 |
∴y+2
| 3 |
∴y=a-2
| 3 |
求得0<x≤
| ||
| 6 |
(3)当⊙Ol和⊙O2外切时,OlO2=2x,2x=a-2
| 3 |
∴x=(
| 3 |
| a |
| 4 |
(4)当DE是△ABC的中位线时,求得x=
| ||
| 8 |
此时BM'=
| 3 |
| 3 |
| 8 |
⊙O1的圆心O1所经过的路线是与△ABC相似,且各边与△ABC各边距离为
| ||
| 8 |
其边长为a-
| 3 |
| 8 |
| a |
| 4 |
∴所求的圆心O1走过的长度为:
| a |
| 4 |
| 3 |
| 4 |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
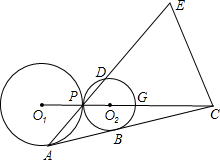 长线上有一点E,满足
长线上有一点E,满足