题目内容
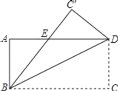
【题目】如图,矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于点E,AD=4,AB=3,求AE的长.
【答案】![]()
【解析】
先根据折叠的性质得到∠DBC=∠DBE,再由AD∥BC得到∠DBC=∠BDE,则∠DBE=∠BDE,于是可判断BE=DE,设AE=x,则DE=BE=4x,然后在Rt△ABE中利用勾股定理得到x2+32=(4x)2,再解方程即可.
解:∵△BDC′是由△BDC折叠得到,
∴∠DBC=∠DBE,
∵AD∥BC,
∴∠DBC=∠BDE,
∴∠DBE=∠BDE,
∴BE=DE
设AE=x,则DE=ADAE=4x,BE=4x,
在Rt△ABE中,∵AE2+AB2=BE2,
∴x2+32=(4x)2,解得x=![]() ,
,
即AE的长为![]() .
.

练习册系列答案
相关题目
【题目】请阅读下列材料,并解答相应的问题:
幻方
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”.中国古代称“幻方”为“河图”、“洛书”等.例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.

(1)设下面的三阶幻方中间的数字是x(其中x为正整数),请用含x的代数式将下面的幻方填充完整.
x+3 | x﹣4 | |
x﹣2 | x | |
x﹣1 | x﹣3 |
(2)若设(1)题幻方中9个数的和为S,则S与中间的数字x之间的数量关系为 .
(3)请在下面的A、B两题中任选一题作答,我选择 .
现要用9个数3,4,5,6,7,8,9,10,11构造一个三阶幻方.
A、幻方最中间的数字应等于 .
B、请将构造的幻方填写在下面3×3的方格中.




