Question

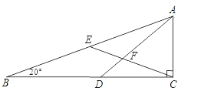
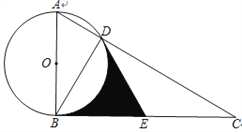
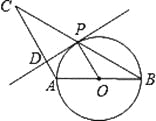
【题目】如图，点P为△ABC的内心，延长AP交△ABC的外接圆⊙O于D，过D作DE∥BC，交AC的延长线于E点．①则直线DE与⊙O的位置关系是_____；②若AB＝4，AD＝6，CE＝3，则DE＝_____．

Answer 1

【答案】相切

【解析】

①连接OD，根据内心的性质得到∠BAD=∠DAE，再根据圆周角的推论得到，利用垂径定理得到OD⊥BC，而DE∥BC，即可得到OD⊥DE；

②连接BD，DC，由BC∥DE，得到∠E=∠ACB，∠BCD=∠CDE，根据同弧所对的圆周角相等得到∠ACB=∠ADB，∠BCD=∠BAD，因此∠E=∠ADB，∠CDE=∠BAD，得到△CDE∽△BAD，则，而AB=4，AD=6，CE=3，BD=DC，先计算出CD，再计算出DE．

解：①连OD，如图，

∵点P为△ABC的内心，

∴∠BAD=∠DAE，

∴，

∴OD⊥BC，

而DE∥BC，

∴OD⊥DE，

∴DE是⊙O的切线；

②连BD，DC，如图，

则BD=CD，

∵BC∥DE，

∴∠E=∠ACB，∠BCD=∠CDE，

而∠ACB=∠ADB，∠BCD=∠BAD，

∴∠E=∠ADB，∠CDE=∠BAD，

∴△CDE∽△BAD，

∴

而AB=4，AD=6，CE=3，BD=CD，

∴，

∴CD=2，则DE=3．

故答案为：相切；3．