题目内容
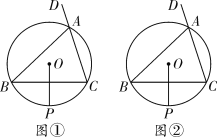
【题目】如图,△ABC是⊙O的内接三角形,∠BAD是它的一个外角,OP⊥BC交⊙O于点P,仅用无刻度的直尺按下列要求分别画图.(保留作图痕迹,不写作法)
(1)在图①中,画出△ABC的角平分线AF;
(2)在图②中,画出△ABC的外角∠BAD的角平分线AG.
【答案】(1)见解析;(2)见解析.
【解析】
(1)连结AP交BC于F,根据垂径定理得到![]() ,则∠BAP=∠CAP,所以AF为△ABC的角平分线;
,则∠BAP=∠CAP,所以AF为△ABC的角平分线;
(2)延长PO交⊙O于G,连结GB、GC,根据垂径定理得GP垂直平分BC,则GB=GC,于是∠GBC=∠GCB,根据圆内接四边形的性质得∠DAG=∠GBC,根据圆周角定理得∠GAB=∠GCB,所以∠DAG=∠GAB,即AG平分∠BAD.
(1)如图①,连接AP交BC于点F,由垂径定理及圆周角的关系,得到∠BAP=∠CAP,AF即为所求;
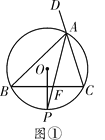
(2)如图②,延长PO交圆于点G,由圆的基本性质知∠PAG为直角,在(1)的基础上可得到∠DAG=∠BAG,则AG即为所求.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目