Question

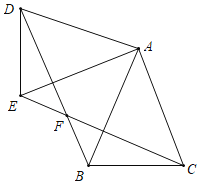
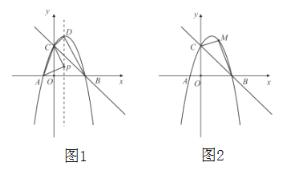
【题目】如图，在正方形ABCD内有一折线段，其中AE⊥EF，EF⊥FC，并且AE＝6，EF＝8，FC＝10，则正方形的边长为_____．

Answer 1

【答案】4．

【解析】

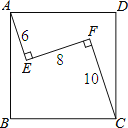
连接AC交EF于点M，可证得△AEM∽△CFM，根据相似三角形的对应边成比例，即可求得EM、FM的长，然后根据勾股定理可得AM、CM，进而可得AC的长，在Rt△ABC中，由AB＝ACsin45°即可求出正方形的边长．

连接AC交EF于点M，

∵AE⊥EF，EF⊥FC，

∴∠E＝∠F＝90°，

∵∠AME＝∠CMF，

∴△AEM∽△CFM，

∴

∵AE＝6，EF＝8，FC＝10，

∴，

∴EM＝3，FM＝5，

在Rt△AEM中，AM＝＝，

在Rt△FCM中，CM＝＝，

∴AC＝，

在Rt△ABC中，AB＝ACsin45°＝×＝，

故答案为：．