Question

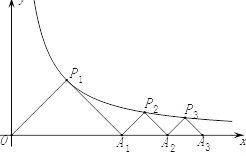
【题目】如图，点P1（x1，y1），点P2（x2，y2），…，点Pn（xn，yn）在函数y＝（x＞0）的图象上，△P1OA1， △P2A1A2，△P3A2A3，…，△PnAn﹣1An都是等腰直角三角形，斜边OA1、A1A2、A2A3，…，An﹣1An都在x轴上（n是大于或等于2的正整数），

(1)求点P1， P2， P3的坐标．

(2)猜想并直接写出点Pn的坐标（用含n的式子表示）．

Answer 1

【答案】(1)求点P1(1，1)， P2(＋1， －1)， P3(＋， －)； (2)点Pn(＋， －)．

【解析】试题分析：根据等腰直角三角形的性质，知P1的横、纵坐标相等，再结合双曲线的解析式求得该点的横、纵坐标，根据等腰直角三角形的性质和双曲线的解析式首先求得各个点的横坐标，再进一步求得其纵坐标，发现其中的规律，从而得到答案．

解：过点P1作P1E⊥x轴于点E，过点P2作P2F⊥x轴于点F，过点P3作P3G⊥x轴于点G，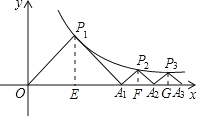

∵△P1OA1是等腰直角三角形，
∴P1E=OE=A1E=OA1，
设点P1的坐标为（a，a），（a＞0），
将点P1（a，a）代入y=，可得a=1，
故点P1的坐标为（1，1），
则OA1=2a，
设点P2的坐标为（b+2，b），将点P2（b+2，b）代入y=，可得b=-1，
故点P2的坐标为（+1， -1），
则A1F=A2F=-1，OA2=OA1+A1A2=2，
设点P3的坐标为（c+2，c），将点P3（c+2，c）代入y=，可得c=－，
故点P3的坐标为（＋， －），
综上可得：P1的坐标为（1，1），P2的坐标为（＋1， －1），P3的坐标为（＋， －），
总结规律可得：Pn坐标为：(＋， －)．