Question

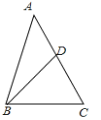
【题目】已知△ABC与△CDE都是等腰直角三角形，∠ACB＝90°，∠DCE＝90°，连结BE，AD，相交于点F．求证：

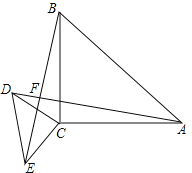
（1）AD＝BE；

（2）AD⊥BE．

Answer 1

【答案】(1)见解析；（2）见解析.

【解析】

（1）根据等腰直角三角形的性质得到∠ECD＝∠ACB＝90°，CD＝CE，CA＝CB，则有∠BCE＝∠DCA，根据“SAS”可判断△BCE≌△ACD，根据全等三角形的性质得到BE＝AD；

（2）由△BCE≌△ACD得到∠CBF＝∠CAD，然后根据∠ABC+∠CAD+∠BAD＝90°，得到∠ABC+∠CBF+∠BAD＝90°，最后根据三角形的内角和定理可知∠AFB＝90°．

证明：（1）∵△ABC与△CDE都是等腰直角三角形

∴CE＝CD，CB＝CA，∠DCE＝∠ACB＝90°．

∴∠DCE+∠BCD＝∠ACB+∠BCD．

∴∠ECB＝∠DCA．

在△BCE和△ACD中，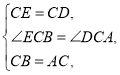

∴△BCE≌△ACD（SAS）．

∴BE＝AD．

（2）由（1）得：△BCE≌△ACD

∴∠CBF＝∠CAD．

∵∠ABC+∠CAD+∠BAD＝90°，

∴∠ABC+∠CBF+∠BAD＝90°．

∴∠AFB＝90°．

∴AD⊥BE．