题目内容
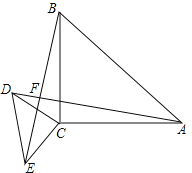
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,分别过点B、C两点作过点A的直线的垂线,垂足为M、N.

(1)如图1,当M、N两点在直线BC的同侧时,求证:BM+CN=MN;
(2)如图2,当M、N两点在直线BC的两侧时,BM、CN、MN三条线段的数量关系并证明.
【答案】(1)见解析;(2)见解析.
【解析】
(1)由垂线的定义和角的互余关系得出∠AMB=∠CNA=90°,∠ABM=∠CAN,由AAS证明△ABM≌△CAN,得出对应边相等BM=AN,AM=CN,由AN+AM=MN,即可得出结论;
(2)由垂线的定义和角的互余关系得出∠AMB=∠CNA=90°,∠ABM=∠CAN,由AAS证明△ABM≌△CAN,得出对应边相等BM=AN,AM=CN,由AN+MN=AM,即可得出结论.
(1)证明:∵∠BAC=90°,
∴∠BAM+∠CAN=90°,
∵BM⊥l,BN⊥l,
∴∠AMB=∠CNA=90°,
∴∠BAM+∠ABM=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,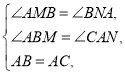
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵AN+AM=MN,
∴BM+CN=MN;
(2)解:BM+MN=CN;理由如下:
∵∠BAC=90°,
∴∠BAM+∠CAN=90°,
∵BM⊥l,BN⊥l,
∴∠AMB=∠BNA=90°,
∴∠BAM+∠ABM=90°,
∴∠ABM=∠CAN,
在△ABM和△CAN中,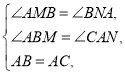 ,
,
∴△ABM≌△CAN(AAS),
∴BM=AN,AM=CN,
∵AN+MN=AM,
∴BM+MN=CN.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案【题目】已知一圆形零件的标准直径是![]() ,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
,超过规定直径长度的数量(毫米)记作正数,不足规定直径长度的数量(毫米)记作负数,检验员某次抽查了零件样品,检查的结果如下:
序号 |
|
|
|
|
|
直径长度/ |
|
|
|
|
|
(1)试指出哪件样品的大小最符合要求?
(2)如果规定误差的绝对值在![]() 之内是正品.误差的绝对值在
之内是正品.误差的绝对值在![]() 之间是次品,误差的绝对值超过
之间是次品,误差的绝对值超过![]() 的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?
的是废品,那么上述五件样品中,哪些是正品,哪些是次品,哪些是废品?