题目内容
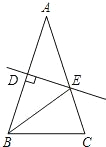
如图，在△ABC中，BO平分∠ABC，CO平分∠ACB，MN∥BC，MN过点O．若AB=12，AC=18，则△AMN的周长是______．
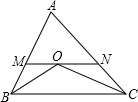
∵BO平分∠CBA，CO平分∠ACB，
∴∠MBO=∠OBC，∠OCN=∠OCB，
∵MN∥BC，
∴∠MOB=∠OBC，∠NOC=∠OCB，
∴∠MBO=∠MOB，∠NOC=∠NCO，
∴NO=NC，MO=MB，
∵AB=12，AC=18，
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30．
故答案为30．
∴∠MBO=∠OBC，∠OCN=∠OCB，
∵MN∥BC，
∴∠MOB=∠OBC，∠NOC=∠OCB，
∴∠MBO=∠MOB，∠NOC=∠NCO，
∴NO=NC，MO=MB，
∵AB=12，AC=18，
∴△AMN的周长=AM+MN+AN=AB+AC=12+18=30．
故答案为30．
练习册系列答案
名校名师培优作业本加核心试卷系列答案
全程金卷系列答案
相关题目
