题目内容
【题目】等边三角形ABC内有一点P,连接AP、BP、CP,若∠BPC=150°,BP=3,AP=5,则CP=_____.
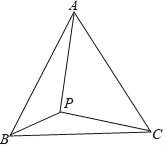
【答案】4
【解析】
将△BCP绕点C顺时针旋转60°得到△ACP′,根据旋转的性质可得BP=AP′,∠AP′C=∠BPC,△PCP′是等边三角形,根据等边三角形的性质可得∠PP′C=60°,然后求出∠AP′P=90°,利用勾股定理列式求出PP′,再根据等边三角形的三边都相等可得CP=PP′.
如图,
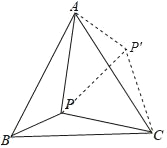
将△BCP绕点C顺时针旋转60°得到△ACP′,
由旋转的性质得,BP=AP′=3,∠AP′C=∠BPC=150°,△PCP′是等边三角形,
所以,∠PP′C=60°,
所以,∠AP′P=∠AP′C﹣∠PP′C=150°﹣60°=90°,
在Rt△APP′中,根据勾股定理得,PP′=![]() =4,
=4,
∵△PCP′是等边三角形,
∴CP=PP′=4.
故答案为:4.

【题目】某企业生产了一款健身器材,可通过实体店和网上商店两种途径进行销售,销售了一段时间后,该企业对这种健身器材的销售情况进行了为期30天的跟踪调查,其中实体店的日销售量y1(套)与时间x(x为整数,单位:天)的部分对应值如下表所示:
时间x(天) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
日销售量y(套) | 0 | 25 | 40 | 45 | 40 | 25 | 0 |
(1)求出y1与x的二次函数关系式及自变量x的取值范围
(2)若网上商店的日销售量y2(套)与时间x(x为整数,单位:天)的函数关系为![]() ,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
,则在跟踪调查的30天中,设实体店和网上商店的日销售总量为y(套),求y与x的函数关系式;当x为何值时,日销售总量y达到最大,并写出此时的最大值.
【题目】如图1,点C是⊙O中直径AB上的一个动点,过点C作CD⊥AB交⊙O于点D,点M是直径AB上一固定点,作射线DM交⊙O于点N.已知AB=6cm,AM=2cm,设线段AC的长度为xcm,线段MN的长度为ycm.
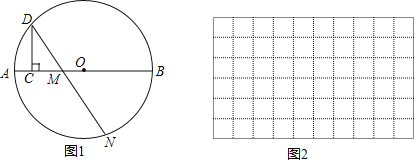
小东根据学习函数的经验,对函数y随自变量的变化而变化的规律进行了探索.
下面是小东的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 4 | 3.3 | 2.8 | 2.5 | 2.1 | 2 |
(说明:补全表格时相关数值保留一位小数)
(2)在图2中建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:当AC=MN时,x的取值约为 cm.