题目内容
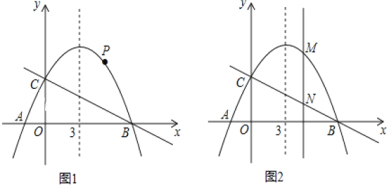
【题目】如图, 已知抛物线![]() 的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
的对称轴是直线x=3,且与x轴相交于A,B两点(B点在A点右侧)与y轴交于C点 .
(1)求抛物线的解析式和A、B两点的坐标;
(2)若点P是抛物线上B、C两点之间的一个动点(不与B、C重合),则是否存在一点P,使△PBC的面积最大.若存在,请求出△PBC的最大面积;若不存在,试说明理由;
(3)若M是抛物线上任意一点,过点M作y轴的平行线,交直线BC于点N,当MN=3时,求M点的坐标 .
【答案】(1)![]() ,点A的坐标为(-2,0),点B的坐标为(8,0);(2)存在点P,使△PBC的面积最大,最大面积是16,理由见解析;(3)点M的坐标为(4-2
,点A的坐标为(-2,0),点B的坐标为(8,0);(2)存在点P,使△PBC的面积最大,最大面积是16,理由见解析;(3)点M的坐标为(4-2![]() ,
,![]() )、(2,6)、(6,4)或(4+2
)、(2,6)、(6,4)或(4+2![]() ,-
,-![]() ).
).
【解析】
(1) 由抛物线的对称轴为直线x=3,利用二次函数的性质即可求出a值, 进而可得出抛物线的解析式, 再利用二次函数图象上点的坐标特征, 即可求出点A、B的坐标;
(2) 利用二次函数图象上点的坐标特征可求出点C的坐标, 由点B、C的坐标, 利用待定系数法即可求出直线BC的解析式, 假设存在, 设点P的坐标为(x,![]() ),过点P作PD//y轴, 交直线BC于点D,则点D的坐标为(x,
),过点P作PD//y轴, 交直线BC于点D,则点D的坐标为(x,![]() ),PD=-
),PD=-![]() x2+2x,利用三角形的面积公式即可得出三角形PBC的面积关于x的函数关系式, 再利用二次函数的性质即可解决最值问题;
x2+2x,利用三角形的面积公式即可得出三角形PBC的面积关于x的函数关系式, 再利用二次函数的性质即可解决最值问题;
(3) 设点M的坐标为(m,![]() ),则点N的坐标为(m,
),则点N的坐标为(m,![]() ),进而可得出MN
),进而可得出MN![]() ,结合MN=3即可得出关于m的含绝对值符号的一元二次方程, 解之即可得出结论 .
,结合MN=3即可得出关于m的含绝对值符号的一元二次方程, 解之即可得出结论 .
(1)![]() 抛物线
抛物线![]() 的对称轴是直线
的对称轴是直线![]() ,
,
![]() ,解得:
,解得:![]() ,
,
![]() 抛物线的解析式为
抛物线的解析式为![]() .
.
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(2) 当![]() 时,
时,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() .
.
设直线![]() 的解析式为
的解析式为![]() .
.
将![]() 、
、![]() 代入
代入![]() ,
,
![]() ,解得:
,解得: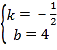 ,
,
![]() 直线
直线![]() 的解析式为
的解析式为![]() .
.
假设存在, 设点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作
作![]() 轴, 交直线
轴, 交直线![]() 于点
于点![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,如图所示 .
,如图所示 .
![]() ,
,
![]() .
.
![]() ,
,
![]() 当
当![]() 时,
时,![]() 的面积最大, 最大面积是 16 .
的面积最大, 最大面积是 16 .
![]() ,
,
![]() 存在点
存在点![]() ,使
,使![]() 的面积最大, 最大面积是 16 .
的面积最大, 最大面积是 16 .
(3) 设点![]() 的坐标为
的坐标为![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
当![]() 时, 有
时, 有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() 或
或![]() ;
;
当![]() 或
或![]() 时, 有
时, 有![]() ,
,
解得:![]() ,
,![]() ,
,
![]() 点
点![]() 的坐标为
的坐标为![]() ,
,![]() 或
或![]() ,
,![]() .
.
综上所述:![]() 点的坐标为
点的坐标为![]() ,
,![]() 、
、![]() 、
、![]() 或
或![]() ,
,![]() .
.