题目内容
【题目】一根竹竿长![]() 米,先像
米,先像![]() 靠墙放置,与水平夹角为
靠墙放置,与水平夹角为![]() ,为了减少占地空间,现将竹竿像
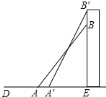
,为了减少占地空间,现将竹竿像![]() 放置,与水平夹角为
放置,与水平夹角为![]() ,则竹竿让出多少水平空间( )
,则竹竿让出多少水平空间( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
先在Rt△ABE中,由∠BAE=45°可判断△ABE为等腰直角三角形,则AE=![]() =
=![]() ,再在Rt△A′B′E中,利用余弦的定义可计算出A′E=acos60°=
,再在Rt△A′B′E中,利用余弦的定义可计算出A′E=acos60°=![]() a,然后计算AA′=AE-A′E即可.
a,然后计算AA′=AE-A′E即可.
在Rt△ABE中,∵∠BAE=45°,
∴△ABE为等腰直角三角形,
∴AE=![]() =
=![]() ,
,
在Rt△A′B′E中,∵cos∠B′A′E= ![]()
而∠B′A′E=60°,A′B′=a,
∴A′E=a·cos60°=![]() a,
a,
∴AA′=AEA′E=![]() -
-![]() a=
a=![]() a (米).
a (米).
即竹竿让出![]() a米的水平空间
a米的水平空间
故选A.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
【题目】某水果基地计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.
甲 | 乙 | 丙 | |
每辆汽车能装的数量(吨) | 4 | 2 | 3 |
每吨水果可获利润(千元) | 5 | 7 | 4 |
(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?