Question

【题目】已知二次函数的顶点坐标为，.

（1）若该函数图象过点.

①求该函数解析式；

②，函数图象上点到x轴的距离最小值为1，则t的值为______；

（2）若点P在函数的图象上，且，求h的最大值.

Answer 1

【答案】（1）①；②或；（2）2

【解析】

（1）①设解析式为，将代入即可求解；

②当抛物线在x轴上方的点到x轴的距离为1时，y=1，

求出横坐标，即可知函数图象上点到x轴的距离最小值为1时的范围，于是可解；

（2）设解析式为，由知图象过，所以.因为点P在函数的图象上，所以，即，分析增减趋势即可求出h的最大值.

解：（1）①设解析式为，将代入,

得，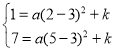

解得，

所以，解析式为，即

②抛物线的顶点为（3，-1），所以抛物线在x轴下方的点到x轴的最大距离为1，不符合题意；

当抛物线在x轴上方的点到x轴的距离为1时，y=1，

即，

解得，，

所以或，函数图象上点到x轴的距离最小值为1，

所以或.

（2）设解析式为，由知图象过，所以.

因为点P在函数的图象上，所以

所以，

因为，所以

因为，h随a的增大而减小，

所以，当时，h的值最大，h的最大值为2.