题目内容
【题目】如图，二次函数
的图象经过点
，
，下列说法正确的是（ ）
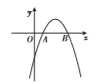
A.
B.
C.
D.图象的对称轴是直线
【答案】D
【解析】
二次函数y=ax2+bx+c（a≠0）
①常数项c决定抛物线与y轴交点．抛物线与y轴交于（0，c）．
②抛物线与x轴交点个数．
△=b2﹣4ac＞0时，抛物线与x轴有2个交点；△=b2﹣4ac=0时，抛物线与x轴有1个交点；△=b2﹣4ac＜0时，抛物线与x轴没有交点．
③根据x=-1时y的值确定a-b+c的符号．
④根据抛物线与x轴的两个交点坐标确定对称轴．
A．由于二次函数y=ax2+bx+c的图象与y轴交于负半轴，所以c＜0，故A错误；
B．二次函数y=ax2+bx+c的图象与x轴由2个交点，所以b2﹣4ac＞0，故B错误；
C．当x=﹣1时，y＜0，即a﹣b+c＜0，故C错误；
D．因为A（1，0），B（4，0），所以对称轴为直线x
，故D正确．
故选D．
练习册系列答案
相关题目
