ЬтФПФкШн
ЁОЬтФПЁПЃЈ1ЃЉЮЪЬтЗЂЯж
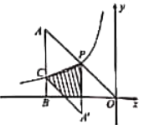
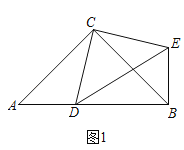
ШчЭМ1ЃЌдкRtЁїABCКЭRtЁїCDEжаЃЌЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН45ЁуЃЌЕуDЪБЯпЖЮABЩЯвЛЖЏЕуЃЌСЌНгBEЃЎ
ЬюПеЃКЂй![]() ЕФжЕЮЊЁЁ ЁЁЃЛ ЂкЁЯDBEЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЕФжЕЮЊЁЁ ЁЁЃЛ ЂкЁЯDBEЕФЖШЪ§ЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉРрБШЬНОП
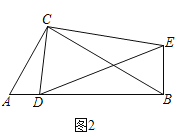
ШчЭМ2ЃЌдкRtЁїABCКЭRtЁїCDEжаЃЌЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌЕуDЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌСЌНгBEЃЎЧыХаЖЯ![]() ЕФжЕМАЁЯDBEЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЕФжЕМАЁЯDBEЕФЖШЪ§ЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ3ЃЉЭиеЙбгЩь
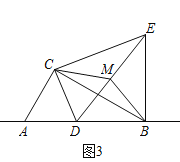
ШчЭМ3ЃЌдкЃЈ2ЃЉЕФЬѕМўЯТЃЌНЋЕуDИФЮЊжБЯпABЩЯвЛЖЏЕуЃЌЦфгрЬѕМўВЛБфЃЌШЁЯпЖЮDEЕФжаЕуMЃЌСЌНгBMЁЂCMЃЌШєACЃН2ЃЌдђЕБЁїCBMЪЧжБНЧШ§НЧаЮЪБЃЌЯпЖЮBEЕФГЄЪЧЖрЩйЃПЧыжБНгаДГіД№АИЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй1ЃЛ Ђк90ЁуЃЛЃЈ2ЃЉ![]() ЃН
ЃН![]() ЃЌЁЯDBEЃН90ЁуЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBEЕФГЄЮЊ3+
ЃЌЁЯDBEЃН90ЁуЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉBEЕФГЄЮЊ3+![]() Лђ3Љ
Лђ3Љ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉгЩжБНЧШ§НЧаЮЕФаджЪПЩЕУЁЯABCЃН45ЁуЃЌПЩЕУЁЯDBEЃН90ЁуЃЌЭЈЙ§жЄУїЁїACDЁзЁїBCEЃЌПЩЕУ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЭЈЙ§жЄУїЁїACDЁзЁїBCEЃЌПЩЕУ![]() ЕФжЕЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌМДПЩЧѓЁЯDBEЕФЖШЪ§ЃЛ
ЕФжЕЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌМДПЩЧѓЁЯDBEЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЗжЕуDдкЯпЖЮABЩЯКЭBAбгГЄЯпЩЯСНжжЧщПіЬжТлЃЌгЩжБНЧШ§НЧаЮЕФаджЪПЩжЄCMЃНBMЃН![]() ЃЌМДПЩЧѓDEЃН2
ЃЌМДПЩЧѓDEЃН2![]() ЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЁЯABEЃН90ЁуЃЌBEЃН
ЃЌгЩЯрЫЦШ§НЧаЮЕФаджЪПЩЕУЁЯABEЃН90ЁуЃЌBEЃН![]() ADЃЌгЩЙДЙЩЖЈРэПЩЧѓBEЕФГЄЃЎ
ADЃЌгЩЙДЙЩЖЈРэПЩЧѓBEЕФГЄЃЎ
НтЃКЃЈ1ЃЉЁпЁЯACBЃН90ЁуЃЌЁЯCABЃН45ЁуЃЌ
ЁрЁЯABCЃНЁЯCABЃН45ЁуЃЌ
ЁрACЃНBCЃЌЁЯDBEЃНЁЯABC+ЁЯCBEЃН90ЁуЃЌ
ЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌЧвЁЯCABЃНЁЯCDEЃН45ЁуЃЌ
ЁрЁїACDЁзЁїBCEЃЌ
Ёр![]() ЃЌ
ЃЌ
ЙЪД№АИЮЊЃК1ЃЌ90ЁуЃЛ
ЃЈ2ЃЉ![]() ЃЌЁЯDBEЃН90ЁуЃЛ
ЃЌЁЯDBEЃН90ЁуЃЛ
РэгЩЃКЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌ
ЁрЁЯACDЃНЁЯBCEЃЌЁЯCEDЃНЁЯABCЃН30ЁуЃЌ
ЁрtanЁЯABCЃНtan30ЁуЃН![]() ЃН
ЃН![]() ЃЌ
ЃЌ
ЁпЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯCABЃНЁЯCDEЃН60ЁуЃЌ
ЁрRtЁїACBЁзRtЁїDCEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЃЌЧвЁЯACDЃНЁЯBCEЃЌ
ЁрЁїACDЁзЁїBCEЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌ
ЃЌЁЯCBEЃНЁЯCADЃН60ЁуЃЌ
ЁрЁЯDBEЃНЁЯABC+ЁЯCBEЃН90ЁуЃЛ
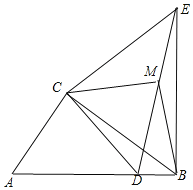
ЃЈ3ЃЉШєЕуDдкЯпЖЮABЩЯЃЌШчЭМЃЌ
гЩЃЈ2ЃЉжЊЃК![]() ЃН
ЃН![]() ЃЌЁЯABEЃН90ЁуЃЌ
ЃЌЁЯABEЃН90ЁуЃЌ
ЁрBEЃН![]() ADЃЌ
ADЃЌ
ЁпACЃН2ЃЌЁЯACBЃН90ЁуЃЌЁЯCABЃН90ЁуЃЌ
ЁрABЃН4ЃЌBCЃН2![]() ЃЌ
ЃЌ
ЁпЁЯECDЃНЁЯABEЃН90ЁуЃЌЧвЕуMЪЧDEжаЕуЃЌ
ЁрCMЃНBMЃН![]() DEЃЌ
DEЃЌ
ЧвЁїCBMЪЧжБНЧШ§НЧаЮЃЌ
ЁрCM2+BM2ЃНBC2ЃНЃЈ2![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁрBMЃНCMЃН![]() ЃЌ
ЃЌ
ЁрDEЃН2![]() ЃЌ
ЃЌ
ЁпDB2+BE2ЃНDE2ЃЌ
ЁрЃЈ4ЉADЃЉ2+ЃЈ![]() ADЃЉ2ЃН24ЃЌ
ADЃЉ2ЃН24ЃЌ
ЁрADЃН![]() +1ЃЌ
+1ЃЌ
ЁрBEЃН![]() ADЃН3+
ADЃН3+![]() ЃЛ
ЃЛ
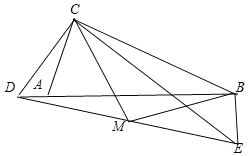
ШєЕуDдкЯпЖЮBAбгГЄЯпЩЯЃЌШчЭМЃЌ
ЭЌРэПЩЕУЃКDEЃН2![]() ЃЌBEЃН
ЃЌBEЃН![]() ADЃЌ
ADЃЌ
ЁпBD2+BE2ЃНDE2ЃЌ
ЁрЃЈ4+ADЃЉ2+ЃЈ![]() ADЃЉ2ЃН24ЃЌ
ADЃЉ2ЃН24ЃЌ
ЁрADЃН![]() Љ1ЃЌ
Љ1ЃЌ
ЁрBEЃН![]() ADЃН3Љ
ADЃН3Љ![]() ЃЌ
ЃЌ
злЩЯЫљЪіЃКBEЕФГЄЮЊ3+![]() Лђ3Љ
Лђ3Љ![]() .
.

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ