题目内容
【题目】已知:如图,点A在y轴上,⊙A与x轴交于B、C两点,与y轴交于点D(0,3)和点E(0,﹣1)
(1)求经过B、E、C三点的二次函数的解析式;
(2)若经过第一、二、三象限的一动直线切⊙A于点P(s,t),与x轴交于点M,连接PA并延长与⊙A交于点Q,设Q点的纵坐标为y,求y关于t的函数关系式,并观察图形写出自变量t的取值范围;
(3)在(2)的条件下,当y=0时,求切线PM的解析式,并借助函数图象,求出(1)中抛物线在切线PM下方的点的横坐标x的取值范围.

【答案】(1)y=![]() x2﹣1(2)y=﹣t+2(1<t<3)(3)
x2﹣1(2)y=﹣t+2(1<t<3)(3)![]() <x<
<x<![]()
【解析】试题分析:(1)已知点D(0,3)和点E(0,-1),可以得到圆的直径,连接AC,根据垂径定理,以及勾股定理就可以求出OB,OE,OC的长度,得到三点的坐标,根据待定系数法就可以求出二次函数的解析式.
(2)过点P作PF⊥y轴于F,过点Q作QN⊥y轴于N,易证△PFA≌△QNA,则FA=NA,即|t-1|=|1-y|,即可得到函数解析式.
(3)当y=0时,Q点与C点重合,连接PB,由PC为 A的直径可以得到PB⊥x轴,就可以求出P点的坐标.求出直线PM的解析式,求出切线PM与抛物线y=![]() x2-1交点坐标,横坐标x的范围就在两个交点之间.
x2-1交点坐标,横坐标x的范围就在两个交点之间.
试题解析:(1)连接AC,
∵DE为⊙A的直径,DE⊥BC,
∴BO=CO,
∵D(0,3),E(0,﹣1),
∴DE=|3﹣(﹣1)|=4,OE=1,
∴AO=1,AC=![]() DE=2,
DE=2,
在Rt△AOC中,AC2=AO2+OC2,
∴OC=![]() ,
,
∴C(![]() ),B(-
),B(-![]() ),
),
设经过B、E、C三点的抛物线的解析式为y=a(x-![]() )(x+
)(x+![]() ),
),
则﹣1=a(0﹣![]() )(0+
)(0+![]() ),
),
解得a=![]() ,
,
∴y=![]() (x﹣
(x﹣![]() )(x+
)(x+![]() )=
)=![]() x2﹣1;
x2﹣1;
(2)过点P作PF⊥y轴于F,过点Q作QN⊥y轴于N,
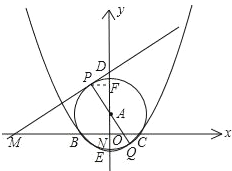
∴∠PFA=∠QNA=90°,F点的纵坐标为t,N点的纵坐标为y,
∵∠PAF=∠QAN,PA=QA,
∴△PFA≌△QNA,
∴FA=NA,
∵AO=1,
∴A(0,1),
∴|t﹣1|=|1﹣y|,
∵动切线PM经过第一、二、三象限
观察图形可得1<t<3,﹣1<y<1;
∴t﹣1=1﹣y.
即y=﹣t+2.
∴y关于t的函数关系式为y=﹣t+2(1<t<3)
(3)当y=0时,Q点与C点重合,连接PB,
∵PC为⊙A的直径,
∴∠PBC=90°,
即PB⊥x轴,
∴s=﹣![]() ,
,
将y=0代入y=﹣t+2(1<t<3),得0=﹣t+2,
∴t=2,P(﹣![]() ,2),
,2),
设切线PM与y轴交于点I,则AP⊥PI,
∴∠API=90°
在△API与△AOC中,
∵∠API=∠AOC=90°,∠PAI=∠OAC
∴△API≌△AOC,
∴![]()
∴I点坐标为(0,5)
设切线PM的解析式为y=kx+5(k≠0),
∵P点的坐标为(﹣![]() ,2),
,2),
∴2=﹣3 k+5.
解得k=![]() ,
,
∴切线PM的解析式为y=![]() x+5,
x+5,
设切线PM与抛物线y=![]() x2﹣1交于G、H两点
x2﹣1交于G、H两点
由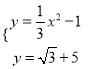 可得x1=
可得x1=![]() ,x2=
,x2=![]() ,
,
因此,G、H的横坐标分别为![]() 、
、![]() ,
,
根据图象可得抛物线在切线PM下方的点的横坐标x的取值范围是![]() <x<
<x<![]() .
.

【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等一系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班
分别选5名同学参加“国防知识”比赛,
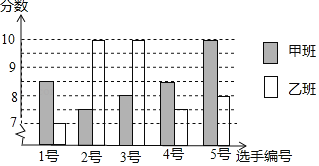
其预赛成绩如图所示:
(1)根据上图填写下表:
平均数 | 中位数 | 众数 | |
甲班 | 8.5 | 8.5 |
|
乙班 | 8.5 |
| 10 |
(2)分别求甲乙两班的方差,并从稳定性上分析哪个班的成绩较好.
【题目】某公司销售部有营销人员15人,销售部为了制定某种商品的月销售定额,统计了这15人某月的销售如下:
每人销售件数 | 1800 | 510 | 250 | 210 | 150 | 120 |
人数 | 1 | 1 | 3 | 5 | 3 | 2 |
(1)求这15位营销人员该月销售量的平均数、中位数和众数.
(2)假设销售部负责人把每位营销员的月销售额定为320件,你认为是否合理?为什么?如不合理,请你制定一个合理的销售定额,并说明理由.