题目内容
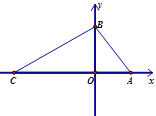
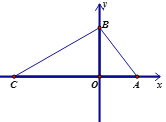
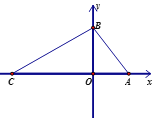
【题目】如图，△ABC的外角∠CBD和∠BCE的平分线相交于点F，则下列结论正确的是（ ）
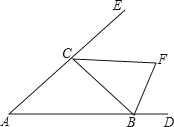
A. 点F在BC边的垂直平分线上 B. 点F在∠BAC的平分线上
C. △BCF是等腰三角形 D. △BCF是直角三角形
【答案】B
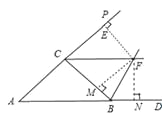
【解析】试题分析：此题主要考查角平分线的性质定理和逆定理．关键是掌握角平分线的性质：角的平分线上的点到角的两边的距离相等．如图，过点F分别作AE、BC、AD的垂线FP、FM、FN，P、M、N为垂足．根据角平分线的性质可得FP=FM，FM=FN．进而得到FP=FN，故点F在∠DAE的平分线上．过点F分别作AE、BC、AD的垂线FP、FM、FN，P、M、N为垂足，由CF是∠BCE的平分线，可得FP=FM；同理可得：FM=FN．∴FP=FN．
∴点F在∠DAE的平分线上．故选：B．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
