题目内容
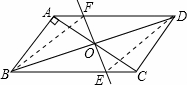
如图,已知在□ABCD中,AB⊥AC,AB=OA,BC= ,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.
,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.

(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试证明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
 ,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.
,对角线AC、BD交于O点,将直线AC绕点O顺时针旋转,分别交BC、AD于点EF.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试证明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不可能,请说明理由;如果可能,说明理由并求出此时AC绕点O顺时针旋转的度数.
(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;
(2)根据平行四边形的性质证得△AOF≌△COE即可;(3)45度.
(2)根据平行四边形的性质证得△AOF≌△COE即可;(3)45度.
试题分析:(1)当旋转角为90°时,∠AOF=90°,由AB⊥AC,可得AB∥EF,即可证明四边形ABEF为平行四边形;
(2)根据平行四边形的性质证得△AOF≌△COE即可;
(3)EF⊥BD时,四边形BEDF为菱形,可根据勾股定理求得AC=2,则OA=1=AB,又AB⊥AC,即可求得结果.
(1)当∠AOF=90°时,AB∥EF,
又∵AF∥BE,
∴四边形ABEF为平行四边形.
(2)∵四边形ABCD为平行四边形,
在△AOF和△COE中
∵∠FAO=∠ECO,AO=CO,∠AOF=∠ECO
∴△AOF≌△COE(ASA)
∴AF=EC;
(3)四边形BEDF可以是菱形.
理由:如图,连接BF,DE
由(2)知△AOF≌△COE,得OE=OF,
∴EF与BD互相平分.
∴当EF⊥BD时,四边形BEDF为菱形.
在Rt△ABC中,
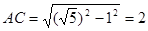
∴OA=1=AB,
又∵AB⊥AC,
∴∠AOB=45°,
∴∠AOF=45°,
∴AC绕点O顺时针旋转45°时,四边形BEDF为菱形.
点评:本题知识点较多,综合性强,是中考常见题,难度不大,学生需熟练掌握平面图形的基本概念.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 中,
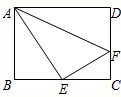
中, , 现将该矩形沿对角线
, 现将该矩形沿对角线 折叠,使得点
折叠,使得点 落在点
落在点 处,
处, 边交
边交 边于点
边于点 ,请求出图中阴影部分的面积.
,请求出图中阴影部分的面积. 

 中,
中, ,
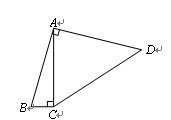
,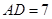 ,∠
,∠ 的平分线交
的平分线交 于点
于点 ,交
,交 的延长线于点
的延长线于点 ,则
,则 的长为
的长为

