题目内容
【题目】如图，所示，四边形ABCD中，AB=4，BC=3，AD=13，CD=12，∠B=90°，求该四边形的面积．
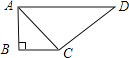
【答案】36．
【解析】
试题分析：由AB=4，BC=3，∠B=90°可得AC=5．可求得S△ABC；再由AC=5，AD=13，CD=12，可得△ACD为直角三角形，进而求得S△ACD，可求S四边形ABCD=S△ABC+S△ACD．
解：在Rt△ABC中，AB=4，BC=3，则有AC=
=5．
∴S△ABC=
ABBC=×4×3=6．
在△ACD中，AC=5，AD=13，CD=12．
∵AC2+CD2=52+122=169，AD2=132=169．
∴AC2+CD2=AD2，∴△ACD为直角三角形，
∴S△ACD=ACCD=×5×12=30．
∴S四边形ABCD=S△ABC+S△ACD=6+30=36．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
