题目内容
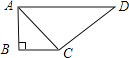
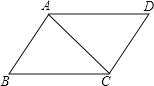
【题目】如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=90°.
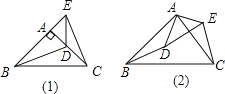
①当点D在AC上时,如图(1),线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;
②将图(1)中的△ADE的位置改变一下,如图(2),使∠BAD=∠CAE,其他条件不变,则线段BD,CE又有怎样的数量关系和位置关系?请说明理由.
【答案】①BD=CE,BD⊥CE;②BD=CE,BD⊥CE,理由见解析
【解析】
试题分析:(1)BD=CE,BD⊥CE,延长BD与EC交于点F,可以证明△ACE≌△ADB,可得BD=CE,且∠BFE=90°,即可解答;
(2)BD=CE,BD⊥CE,延长BD交AC于F,交CE于H,可以证明△ACE≌△ADB,可得BD=CE,利用三角形的内角和为180°,即可得到BD⊥CE.
解:(1)BD=CE,BD⊥CE;
如图(1),延长BD与EC交于点F,
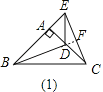
在△ACE和△ADB中,
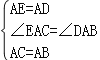 ,
,
∴△ACE≌△ADB(SAS),
∴BD=CE,∠AEC=∠ADB,
∵∠ADB+∠ABD=90°
∴∠ABD+∠AEC=90°
∴∠BFE=90°,
∴BD⊥CE.
(2)结论:BD=CE,BD⊥CE,
理由如下:∵∠BAC=∠DAE=90°
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
即∠BAD=∠CAE,
在△ABD与△ACE中,
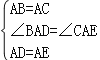
∴△ABD≌△ACE(SAS)
∴BD=CE,
如图(2),延长BD交AC于F,交CE于H.
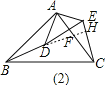
在△ABF与△HCF中,
∵∠ABF=∠HCF,∠AFB=∠HFC
∴∠CHF=∠BAF=90°
∴BD⊥CE.

练习册系列答案
相关题目