Question

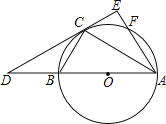
【题目】如图，在平行四边形ABCD中，∠ADB=90°，AB=2AD，BD的垂直平分线分别交AB，CD于点E，F，垂足为O．

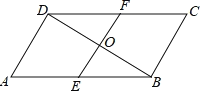
（1）求tan ∠ABD的值；

（2）求证：OE=OF；

（3）连接DE，BF，若AD=6，求DEBF的周长．

Answer 1

【答案】(1) tan∠ABD的值为;(2)见解析；（3）24

【解析】

（1）根据勾股定理和三角函数解答即可；

（2）根据平行四边形的性质和全等三角形的判定和性质证明即可；

（3）先证四边形DEBF是菱形，得到DE=EB=BF=DF．再证∠ABD=30°，进而得到△ADE是等边三角形，得到AE=AD=DE=6，即可得出结论．

（1）设AD=x，∴AB=2AD=2x．

∵∠ADB=90°，∴BD===，∴tan ∠ABD=；

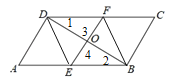
（2）∵四边形ABCD是平行四边形，∴AB∥DC，∴∠1=∠2．

∵EF是BD的中垂线，∴OD=OB，∠3=∠4=90°，∴△DOF≌△BOE，∴OE=OF；

（3）由（2）得：OE=OF，OD=OB，∴四边形DEBF是平行四边形．

∵EF⊥BD，∴四边形DEBF是菱形，∴DE=EB=BF=DF．

∵tan ∠ABD=，∴∠ABD=30°，∴∠A=60°，∠EDB=∠ABD=30°，∴∠ADE=90°－30°=60°，∴△ADE是等边三角形，∴AE=AD=DE=6，∴DEBF的周长=4DE=24．