题目内容
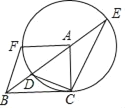
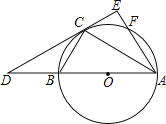
【题目】如图,已知△ABC内接于⊙O,AB是⊙O的直径,点F在⊙O上,且点C是![]() 的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
的中点,过点C作⊙O的切线交AB的延长线于点D,交AF的延长线于点E.
(1)求证:AE⊥DE;
(2)若∠BAF=60°,AF=4,求CE的长.
【答案】(1)见解析;(2)CE=2![]() .
.
【解析】
(1)连接OC,如图,利用切线的性质得OC⊥DE,再利用圆周角定理得到∠BAC=∠EAC,加上∠BAC=∠OCA,所以∠EAC=∠OCA.则OC∥AE,从而得到AE⊥DE;
(2)连接BF交OC于G,如图,利用圆周角定理得到∴∠BFA=90°.易得四边形CEFG是矩形.则CO⊥BF,CF=GF,利用垂径定理得到BG=GF,再在Rt△ABF中利用含30度的直角三角形三边的关系得到BF=![]() AF=4
AF=4![]() ,则BG=GF=2
,则BG=GF=2![]() ,从而得到CE的长.
,从而得到CE的长.
(1)证明:连接OC,如图,
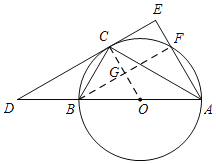
∵DE切⊙O于C,
∴OC⊥DE,
∵点C是![]() 的中点,
的中点,
∴∠BAC=∠EAC,
∵OC=OA,
∴∠BAC=∠OCA,
∴∠EAC=∠OCA.
∴OC∥AE.
∴AE⊥DE;
(2)连接BF交OC于G,如图,
∵AB是⊙O直径,
∴∠BFA=90°.
易得四边形CEFG是矩形.
∴CO⊥BF,CF=GF,
∴BG=GF,
在Rt△ABF中,∠BAE=60°,AF=4,
∴BF=![]() AF=4
AF=4![]() ,
,
∴BG=GF=2![]()
∴CE=2![]() .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目