题目内容
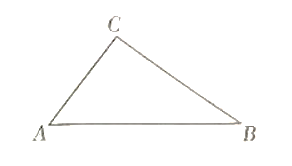
【题目】如图，以
的三边为边分别作等边
、
、
，则下列结论：①①
；②四边形
为平行四边形；③当
时，四边形是菱形；④当
时，四边形是矩形．其中正确的结论有（ ）个．
A. 1 B. 2 C. 3 D. 4
【答案】C
【解析】
①由△ABE与△BCF都为等边三角形，利用等边三角形的性质得到两对边相等，∠ABE＝∠CBF＝60°，利用等式的性质得到夹角相等，利用SAS得到△EBF与△DFC全等；
②利用（1）中全等三角形对应边相等得到EF＝AC，再由三角形ADC为等边三角形得到三边相等，等量代换得到EF＝AD，AE＝DF，利用对边相等的四边形为平行四边形得到AEFD为平行四边形；
③当AE＝AD时，ADFE是菱形，可以用邻边相等的平行四边形是菱形判断即可；
④当∠BAC＝150°，由此可求得∠EAD的度数，则可得ADFE是矩形，由此即可判断；
∵△ABE、△BCF为等边三角形，
∴AB＝BE＝AE，BC＝CF＝FB，∠ABE＝∠CBF＝60°，
∴∠ABE∠ABF＝∠FBC∠ABF，即∠CBA＝∠FBE，
在△ABC和△EBF中，
，
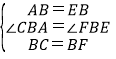∴△ABC≌△EBF（SAS），
∴EF＝AC，
又∵△ADC为等边三角形，
∴CD＝AD＝AC，
∴EF＝AD＝DC，
同理可得△ABC≌△DFC，
∴DF＝AB＝AE＝DF，
∴四边形AEFD是平行四边形；
∴∠FEA＝∠ADF，
∴∠FEA＋∠AEB＝∠ADF＋∠ADC，即∠FEB＝∠CDF，
在△FEB和△CDF中，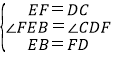
，
∴△EBF≌△DFC（SAS），故①正确，
∴EB＝DF，EF＝DC．
∵△ACD和△ABE为等边三角形，
∴AD＝DC，AE＝BE，
∴AD＝EF，AE＝DF
∴四边形AEFD是平行四边形；故②正确，
若AB＝AC，则AE＝AD，四边形AEFD是菱形此，
故△ABC满足AB＝AC时，四边形AEFD是菱形；故③正确；
若∠BAC＝90°，则平行四边形AEFD是矩形；
由（1）知四边形AEFD是平行四边形，则∠EAD＝90°时，可得平行四边形AEFD是矩形，
∴∠BAC＝360°60°60°90°＝150°，
即△ABC满足∠BAC＝150°时，四边形AEFD是矩形；
∴∠BAC＝90°，四边形AEFD不是矩形；故④错误，
故选：C．
