题目内容
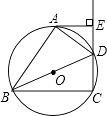
【题目】问题背景: 如图①,在四边形ADBC中,∠ACB=∠ADB=90°,AD=BD,探究线段AC,BC,CD之间的数量关系.
小吴同学探究此问题的思路是:将△BCD绕点D,逆时针旋转90°到△AED处,点B,C分别落在点A,E处(如图②),易证点C,A,E在同一条直线上,并且△CDE是等腰直角三角形,所以CE= ![]() CD,从而得出结论:AC+BC=
CD,从而得出结论:AC+BC= ![]() CD.
CD.
简单应用:
(1)在图①中,若AC= ![]() ,BC=2
,BC=2 ![]() ,则CD= .
,则CD= .
(2)如图③,AB是⊙O的直径,点C、D在⊙上, ![]() =
= ![]() ,若AB=13,BC=12,求CD的长. 拓展规律:
,若AB=13,BC=12,求CD的长. 拓展规律:
(3)如图④,∠ACB=∠ADB=90°,AD=BD,若AC=m,BC=n(m<n),求CD的长(用含m,n的代数式表示)
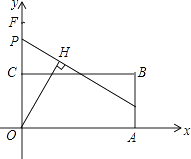
(4)如图⑤,∠ACB=90°,AC=BC,点P为AB的中点,若点E满足AE= ![]() AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 .
AC,CE=CA,点Q为AE的中点,则线段PQ与AC的数量关系是 . 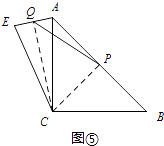
【答案】
(1)3
(2)解:连接AC、BD、AD,

∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
∵ ![]() ,
,
∴AD=BD,
将△BCD绕点D,逆时针旋转90°到△AED处,如图③,
∴∠EAD=∠DBC,
∵∠DBC+∠DAC=180°,
∴∠EAD+∠DAC=180°,
∴E、A、C三点共线,
∵AB=13,BC=12,
∴由勾股定理可求得:AC=5,
∵BC=AE,
∴CE=AE+AC=17,
∵∠EDA=∠CDB,
∴∠EDA+∠ADC=∠CDB+∠ADC,
即∠EDC=∠ADB=90°,
∵CD=ED,
∴△EDC是等腰直角三角形,
∴CE= ![]() CD,
CD,
∴CD= ![]() ;
;
(3)解:以AB为直径作⊙O,连接OD并延长交⊙O于点D1,
连接D1A,D1B,D1C,如图④
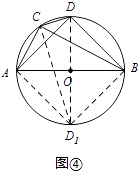
由(2)的证明过程可知:AC+BC= ![]() D1C,
D1C,
∴D1C= ![]() ,
,
又∵D1D是⊙O的直径,
∴∠DCD1=90°,
∵AC=m,BC=n,
∴由勾股定理可求得:AB2=m2+n2,
∴D1D2=AB2=m2+n2,
∵D1C2+CD2=D1D2,
∴CD=m2+n2﹣ ![]() =
= ![]() ,
,
∵m<n,
∴CD= ![]() ;
;
(4)![]() PQ=
PQ= ![]() AC或
AC或 ![]() PQ=
PQ= ![]() AC?
AC?
【解析】解:(1)由题意知:AC+BC= ![]() CD, ∴
CD, ∴ ![]() +2
+2 ![]() =
= ![]() CD,
CD,
∴CD=3;
·(4)当点E在直线AC的左侧时,如图⑤,
连接CQ,PC,
∵AC=BC,∠ACB=90°,
点P是AB的中点,
∴AP=CP,∠APC=90°,
又∵CA=CE,点Q是AE的中点,
∴∠CQA=90°,
设AC=a,
∵AE= ![]() AC,
AC,
∴AE= ![]() a,
a,
∴AQ= ![]() AE=
AE= ![]() ,
,
由勾股定理可求得:CQ= ![]() a,
a,
由(2)的证明过程可知:AQ+CQ= ![]() PQ,
PQ,
∴ ![]() PQ=
PQ= ![]() a+
a+ ![]() a,
a,
∴ ![]() PQ=
PQ= ![]() AC;
AC;
当点E在直线AC的右侧时,如图⑥,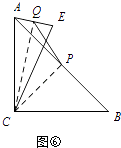
连接CQ、CP,
同理可知:∠AQC=∠APC=90°,
设AC=a,
∴AQ= ![]() AE=
AE= ![]() ,
,
由勾股定理可求得:CQ= ![]() a,
a,
由(3)的结论可知:PQ= ![]() (CQ﹣AQ),
(CQ﹣AQ),
∴ ![]() PQ=
PQ= ![]() AC.
AC.
综上所述,线段PQ与AC的数量关系是 ![]() PQ=
PQ= ![]() AC或
AC或 ![]() PQ=
PQ= ![]() AC.
AC.

【题目】文昌某校准备组织学生及学生家长到三亚进行社会实践,为了便于管理,所有人员必须乘坐在同一列火车上;根据报名人数,若都买一等座单程火车票需17010元,若都买二等座单程火车票且花钱最少,则需11220元;已知学生家长与教师的人数之比为2:1,文昌到三亚的火车票价格(部分)如下表所示:
运行区间 | 公布票价 | 学生票 | ||
上车站 | 下车站 | 一等座 | 二等座 | 二等座 |
文昌 | 三亚 | 81(元) | 68(元) | 51(元) |
(1)参加社会实践的老师、家长与学生各有多少人?
(2)由于各种原因,二等座火车票单程只能买x张(x小于参加社会实践的人数),其余的须买一等座火车票,在保证每位参与人员都有座位坐的前提下,请你设计最经济的购票方案,并写出购买火车票的总费用(单程)y与x之间的函数关系式.
(3)请你做一个预算,按第(2)小题中的购票方案,购买一个单程火车票至少要花多少钱?最多要花多少钱?