��Ŀ����
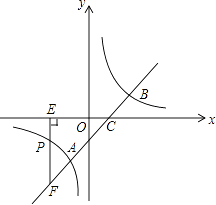
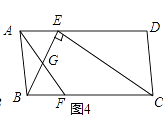
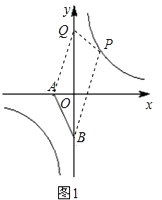
����Ŀ����ͼ1����֪��A��a��0����B��0��b������a��b���� ![]() ��ABCD�ı�AD��y�ύ�ڵ�E����EΪAD�е㣬˫����
��ABCD�ı�AD��y�ύ�ڵ�E����EΪAD�е㣬˫���� ![]() ����C��D���㣮
����C��D���㣮
��1����k��ֵ��
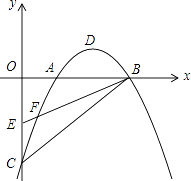
��2����P��˫���� ![]() �ϣ���Q��y���ϣ����Ե�A��B��P��QΪ������ı�����ƽ���ı��Σ���������Ҫ������е�P��Q�����ꣻ
�ϣ���Q��y���ϣ����Ե�A��B��P��QΪ������ı�����ƽ���ı��Σ���������Ҫ������е�P��Q�����ꣻ
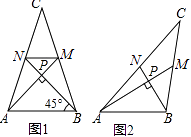
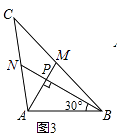
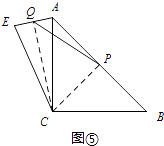
��3�����߶�ABΪ�Խ�����������AFBH����ͼ3������T�DZ�AF��һ���㣬M��HT���е㣬MN��HT����AB��N����T��AF���˶�ʱ�� ![]() ��ֵ�Ƿ����ı䣿���ı䣬�����仯��Χ�������ı䣬�������ֵ�����������֤����
��ֵ�Ƿ����ı䣿���ı䣬�����仯��Χ�������ı䣬�������ֵ�����������֤����
���𰸡�
��1��
�⣺�� ![]() +��a+b+3��2=0����
+��a+b+3��2=0���� ![]() ��0����a+b+3��2��0��
��0����a+b+3��2��0��
�� ![]() ��
��
��ã� ![]() ��
��
��A����1��0����B��0����2����
��EΪAD�е㣬
��xD=1��
��D��1��t����
�֡�DC��AB��
��C��2��t��2����
��t=2t��4��
��t=4��
��k=4��
��2��
�⣺���ɣ�1��֪k=4��
�෴���������Ľ���ʽΪy= ![]() ��
��
�ߵ�P��˫���� ![]() �ϣ���Q��y���ϣ�
�ϣ���Q��y���ϣ�
����Q��0��y����P��x�� ![]() ����
����
�ٵ�ABΪ��ʱ��
��ͼ1��ʾ��
��ABPQΪƽ���ı��Σ��� ![]() =0�����x=1����ʱP1��1��4����Q1��0��6����
=0�����x=1����ʱP1��1��4����Q1��0��6����
��ͼ2��ʾ��
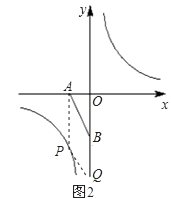
��ABQPΪƽ���ı��Σ��� ![]() =
= ![]() �����x=��1����ʱP2����1����4����Q2��0����6����
�����x=��1����ʱP2����1����4����Q2��0����6����
��ͼ3��ʾ��
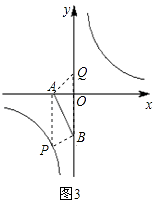
�ڵ�ABΪ�Խ���ʱ��AP=BQ����AP��BQ��
�� ![]() =
= ![]() �����x=��1��
�����x=��1��
��P3����1����4����Q3��0��2����
��P1��1��4����Q1��0��6����P2����1����4����Q2��0����6����P3����1����4����Q3��0��2����
��3��
�⣺��NH��NT��NF��
��MN���߶�HT�Ĵ�ֱƽ���ߣ�
��NT=NH��
���ı���AFBH�������Σ�
���ABF=��ABH��
�ڡ�BFN���BHN�У�
��  ��
��
���BFN�ա�BHN��
��NF=NH=NT��
���NTF=��NFT=��AHN��
�ı���ATNH�У���ATN+��NTF=180�㣬����NTF=��NFT=��AHN��
���ԣ���ATN+��AHN=180�㣬���ԣ��ı���ATNH�ڽǺ�Ϊ360�㣬
���ԡ�TNH=360�㩁180�㩁90��=90�㣮
��MN= ![]() HT��
HT��
�� ![]() =
= ![]() ��
��
����������1���ȸ��ݷǸ������������a��b��ֵ���ʿɵó�A��B��������꣬��D��1��t������DC��AB����֪C��2��t��2�����ٸ��ݷ������������������t��ֵ���ɣ���2���ɣ�1��֪k=4��֪�����������Ľ���ʽΪy= ![]() �����ɵ�P��˫����
�����ɵ�P��˫���� ![]() �ϣ���Q��y���ϣ���Q��0��y����P��x��
�ϣ���Q��y���ϣ���Q��0��y����P��x�� ![]() �����ٷ���ABΪ�ߺ���ABΪ�Խ�������������x��ֵ���ʿɵó�P��Q�����ꣻ��3����NH��NT��NF����֤NF=NH=NT���ʡ�NTF=��NFT=��AHN����TNH=��TAH=90�㣬MN=
�����ٷ���ABΪ�ߺ���ABΪ�Խ�������������x��ֵ���ʿɵó�P��Q�����ꣻ��3����NH��NT��NF����֤NF=NH=NT���ʡ�NTF=��NFT=��AHN����TNH=��TAH=90�㣬MN= ![]() HT�ɴ˼��ɵó����ۣ�
HT�ɴ˼��ɵó����ۣ�
�����㾫�������÷�����������ͼ��ͷ��������������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪������������ͼ������˫���ߣ�������������ͼ�������Գ�ͼ���������ĶԳ�ͼ�Σ��������Գ��ֱ��y=x�� y=-x���Գ������ǣ�ԭ�㣻����:��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵ�һ���������ޣ���ÿ��������yֵ��xֵ���������С�� ��k��0ʱ˫���ߵ���֧�ֱ�λ�ڵڶ����������ޣ���ÿ��������yֵ��xֵ�����������