Question

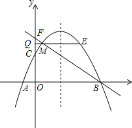
【题目】如图，点P是直线y＝3上的动点，连接PO并将PO绕P点旋转90°到PO′，当点O′刚好落在双曲线（x＞0）上时，点P的横坐标所有可能值为_____．

Answer 1

【答案】，.

【解析】

分点P在由在y轴的左侧和点P在y轴的右侧两种情况求解即可.

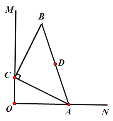
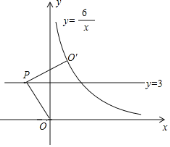
当点P在由在y轴的左侧时，如图1，过点P作PM⊥x轴于点M，过点O′作O′N垂直于直线y=3于点N，

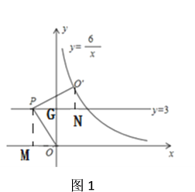
∵∠OPN+∠NP O′=90°，∠P O′N+∠NP O′=90°，

∴∠OPN=∠P O′N，

∵直线y=3与x轴平行，

∴∠POM=∠O P N ，

∴∠POM=∠P O′N，

在△POM和△P O′N中，

，

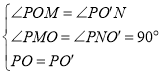∴△POM≌△P O′N，

∴OM= O′N，PM=PN，

设点P的横坐标为t，则OM= O′N=-t，PM=PN=3，

∴GN=3+t，

∴点O′的坐标为（3+t，3-t），

∵点O′在双曲线（x＞0）上，

∴（3+t）（3-t）=6，

解得，t=（舍去）或t=-，

∴点P的横坐标为-；

当点P在由在y轴的右侧时，

如图2，过点O′作O′H垂直于直线y=3于点H，

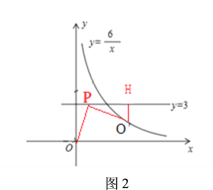
类比图1的方法易求点P的横坐标为，

如图3，过点P作PE⊥x轴于点E，过点O′作O′F垂直于直线y=3于点F，

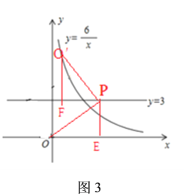
类比图1的方法易求点P的横坐标为，

综上，点P的横坐标为，.

故答案为：，.