题目内容
【题目】如图,长方形纸片ABCD中,AB=4,将纸片折叠,折痕的一个端点F在边AD上,另一个端点G在边BC上,若顶点B的对应点E落在长方形内部,E到AD的距离为1,BG=5,则AF的长为_____.

【答案】![]()
【解析】分析:设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,然后求出EM、EN,在Rt△ENG中,利用勾股定理列式求出GN,再根据△GEN和△EKM相似,利用相似三角形对应边成比例列式求出EK、KM,再求出KH,然后根据△FKH和△EKM相似,利用相似三角形对应边成比例列式求解即可.
详解:设EH与AD相交于点K,过点E作MN∥CD分别交AD、BC于M、N,
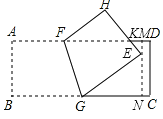
∵E到AD的距离为1,
∴EM=1,EN=4-1=3,
在Rt△ENG中,GN=![]() ,
,
∵∠GEN+∠KEM=180°-∠GEH=180°-90°=90°,
∠GEN+∠NGE=180°-90°=90°,
∴∠KEM=∠NGE,
又∵∠ENG=∠KME=90°,
∴△GEN∽△EKM,
∴![]() ,
,
即![]() ,
,
解得EK=![]() ,KM=
,KM=![]() ,
,
∴KH=EH-EK=4-![]() =
=![]() ,
,
∵∠FKH=∠EKM,∠H=∠EMK=90°,
∴△FKH∽△EKM,
∴![]() ,
,
即  ,
,
解得FH=![]() ,
,
∴AF=FH=![]() .
.
故答案为![]() .
.

 优生乐园系列答案
优生乐园系列答案【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?