题目内容
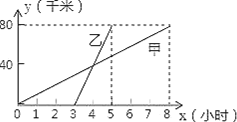
【题目】甲、乙两人分别骑自行车和摩托车沿相同路线由A地到相距80千米的B地,行驶过程中的函数图象如图所示,请根据图象回答下列问题:
(1)甲先出发______小时后,乙才出发;大约在甲出发______小时后,两人相遇,这时他们离A地_______千米.
(2)两人的行驶速度分别是多少?
(3)分别写出表示甲、乙的路程y(千米)与时间x(小时)之间的函数表达式(不要求写出自变量的取值范围).
【答案】(1)3;4;40.(2)甲的速度10km/h;乙的速度40km/h.(3)甲的函数表达式:y=10x;乙的函数表达式:y=40x120.
【解析】
(1)结合图象,由速度=路程÷时间,即可得出结论,求出甲、乙的速度,根据待定系数法,可求出乙的函数表达式,结合甲的速度依据甲的图象过原点,可得出甲的函数表达式;
(2)(3)由(1)所求即可写出结论.
(1)根据图像可得:
甲的速度:80÷8=10km/h;
乙的速度:80÷(53)=40km/h.
∵甲的速度为10km/h,且过原点(0,0),
∴甲的函数表达式:y=10x;
设乙的函数表达式为y=kx+b,
∵点(3,0)和(5,80)在乙的图象上,
∴有![]() ,解得:
,解得:![]() .
.
故乙的函数表达式:y=40x120.
由图可得甲先出发3小时后,乙才出发;
令y=10x=40x120,解得x=4,此时y=40,
∴在甲出发4小时后,两人相遇,这时他们离A地40千米.
故答案为:3;4;40.
(2)由(1)得甲的速度10km/h;乙的速度40km/h.
(3)由(1)甲的函数表达式:y=10x;乙的函数表达式:y=40x120.

 阅读快车系列答案
阅读快车系列答案【题目】快递公司为提高快递分拣的速度,决定购买机器人来代替人工分拣,两种型号的机器人的工作效率和价格如表:
型号 | 甲 | 乙 |
每台每小时分拣快递件数(件) | 1000 | 800 |
每台价格(万元) | 5 | 3 |
该公司计划购买这两种型号的机器人共10台,并且使这10台机器人每小时分拣快递件数总和不少于8500件
(1)设购买甲种型号的机器人x台,购买这10台机器人所花的费用为y万元,求y与x之间的关系式;
(2)购买几台甲种型号的机器人,能使购买这10台机器人所花总费用最少?最少费用是多少?