��Ŀ����
����Ŀ���Ķ����ϣ�������⣮
������ͼ��һԪ���β���ʽ��x2��2x��3��0
�⣺��y=x2��2x��3����y��x�Ķ��κ�������a=1��0���������߿������ϣ�
�֡ߵ�y=0ʱ��x2��2x��3=0�����x1=��1��x2=3��
���ɴ˵�������y=x2��2x��3�Ĵ���ͼ����ͼ��ʾ��
�۲캯��ͼ���֪����x����1��x��3ʱ��y��0��
��x2��2x��3��0�Ľ⼯�ǣ�x����1��x��3��
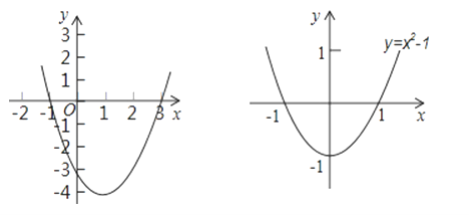
��1���۲�ͼ��ֱ��д��һԪ���β���ʽ��x2��2x��3��0�Ľ⼯�ǡ�________��
��2��������������ͼ��һԪ���β���ʽ��x2��1��0��
���𰸡��⣺��1��x����1��x��3��
��2����y=x2��1����y��x�Ķ��κ�����
��a=1��0��
�������߿������ϣ�
������y=0ʱ��x2��1=0��
���x1=��1��x2=1��
���ɴ˵�������y=x2��1�Ĵ���ͼ����ͼ��ʾ��
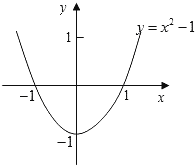
�۲캯��ͼ���֪����x����1��x��1ʱ��y��0��
��x2��1��0�Ľ⼯�ǣ�x����1��x��1��
��������
��1����x2��2x��3=0��x1=��1��x2=3��������y=x2��2x��3�������ϣ�y��0ʱ��ͼ����x����Ϸ�����ʱx����1��x��3��
��2�����գ�1���ķ�������������y=x2��1��ͼ���ҳ�ͼ����x��Ľ������꣬����ͼ��Ŀ��ڷ�����ֵ�ķ��ţ�ȷ��x�ķ�Χ��