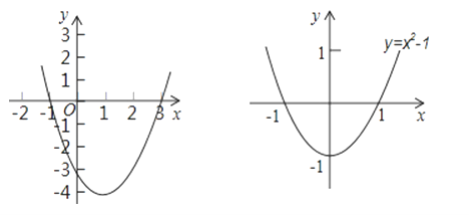题目内容
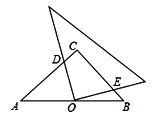
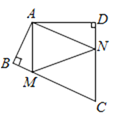
【题目】如图，在四边形ABCD中，∠BAD=130°，∠B=∠D=90°，在BC，CD上分别找一点M，N，使三角形AMN周长最小时，则∠MAN的度数为_________.
【答案】80°
【解析】
延长AB到
,使得B=AB，延长AD到
，使得DA=D，连接、与BC、CD分别交于点M、N，此时 △AMN周长最小，然后因为∠AMN=∠BAD－(∠BAM＋∠DAN)，之后推出∠BAM＋∠DAN的值从而得出答案。
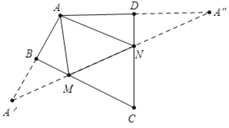
如图，延长AB到,使得B=AB，延长AD到，使得DA=D，连接、与BC、CD分别交于点M、N
∵∠ABC=∠ADC=90°
∴与A关于BC对称；与A关于CD对称
此时△AMN周长最小
∵BA=B，MB⊥AB
∴MA=M
同理：NA=N
∴∠=∠
AM,∠
∵∠＋∠＋∠BAD=180°，且∠BAD=130°
∴∠＋∠=50°
∴∠BAM＋∠DAN=50°
∴∠MAN=∠BAD－(∠BAM＋∠DAN)=130°－50°=80°
所以答案为80°
练习册系列答案
相关题目
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息，完成下列各题：
（1）当x=3时，y=________；
（2）当x=_____时，y有最________值为________；
（3）若点A（x1，y1）、B（x2，y2）是该二次函数图象上的两点，且﹣1＜x1＜0，1＜x2＜2，试比较两函数值的大小：y1________y2 ；
（4）若自变量x的取值范围是0≤x≤5，则函数值y的取值范围是________．
