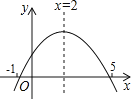题目内容
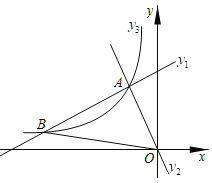
【题目】如图，在平面直角坐标系
中，一次函数
和
的图象相交于点A，反比例函数
的图象经过点A，反比例函数
的图象经过点
．
(1)求反比例函数的表达式；
(2)直接写出
时，x的取值范围；
(3)在x轴上是否存在点P，使△ABP为直角三角形，若存在请求出P点坐标，若不存在，请说明理由．
【答案】（1）y=-
；（2）x＜-8或-2＜x＜0；（3）在x轴上存在点P1（-
、0）P2（0、0）使△PAB为直角三角形
【解析】
（1）联立一次函数
和
，解出A点坐标，代入反比例函数解析式即可求出；
（2）联立和y=-解出B点坐标，结合图像即可得出答案；
（3）假设在x轴上存在P（t、0）使△PAB为直角三角形，用含t的代数式表示PA2，
PB2，AB2，然后根据勾股定理分①PA2+PB2=PC2；②PA2=PB2+PC2；③PB2=PA2+AB2三种情况讨论即可．
（1）解：依题得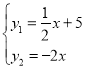
解得
，即A（-2、4）
将A（-2、4）代入
得k=-8，即反比例函数解析式为：y=-；
（2）∵
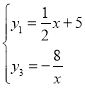
解得：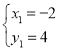
或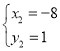
，即B（-8、1）
∴结合图像可得当y1＜y3时，x的取值范围是x＜-8或-2＜x＜0；
（3）如图，假设在x轴上存在P（t、0）使△PAB为直角三角形，
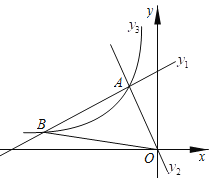
∵ PA2=（t+2）2+42=t2+4t+20
PB2=(t+8)2+1=t2+16t+65
AB2=62+32=45
①PA2+PB2=PC2，即t2+4t+20+t2+16t+65=45
化简得t2+t+1=0
此时方程无解，故此种情况不成立；
②PA2=PB2+PC2 即t2+4t+20=t2+16t+65+45
解得：t=-；
③PB2=PA2+AB2 即t2+16t+65=45+t2+4t+20
解得：t=0；
综上所，在x轴上存在点P1（-、0），P2（0、0）使△PAB为直角三角形．
