ΧβΡΩΡΎ»ί
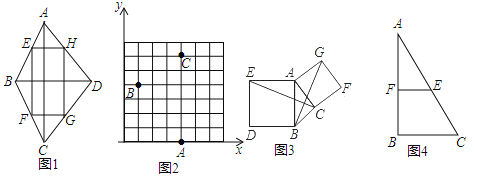
ΓΨΧβΡΩΓΩ»γΆΦ1Θ§»τΥ≥¥ΈΝ§Ϋ”ΥΡ±Ώ–ΈABCDΗς±Ώ÷–ΒψΒΟΒΡΥΡ±Ώ–ΈEFGH «ΨΊ–ΈΘ§‘ρ≥Τ‘≠ΥΡ±Ώ–ΈABCDΈΣΓΑ÷–ΡΗΨΊ–ΈΓ±Φ¥»τΥΡ±Ώ–ΈΒΡΕ‘Ϋ«œΏΜΞœύ¥Ι÷±Θ§Ρ«Ο¥’βΗωΥΡ±Ώ–Έ≥ΤΈΣΓΑ÷–ΡΗΨΊ–ΈΓ±.
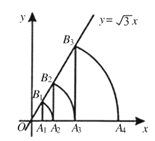
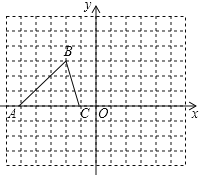
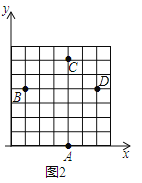
Θ®1Θ©»γΆΦ2Θ§‘Ύ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§“―÷ΣAΘ®4Θ§0Θ©Θ§BΘ®1Θ§4Θ©Θ§CΘ®4Θ§6Θ©Θ§«κ‘ΎΗώΒψ…œ±ξ≥ωDΒψΒΡΈΜ÷ΟΘ®÷Μ±ξ“ΜΒψΦ¥Ω…Θ©Θ§ ΙΥΡ±Ώ–ΈABCD «÷–ΡΗΨΊ–Έ.≤Δ–¥≥ωΒψDΒΡΉχ±ξ.
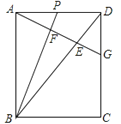
Θ®2Θ©»γΆΦ3Θ§“‘ΓςABCΒΡ±ΏABΘ§ACΈΣ±ΏΘ§œρ»ΐΫ«–ΈΆβΉς’ΐΖΫ–ΈABDEΦΑACFGΘ§Ν§Ϋ”CEΘ§BGœύΫΜ”ΎΒψOΘ§ ‘≈–ΕœΥΡ±Ώ–ΈBEGC «÷–ΡΗΨΊ–ΈΘΩΥΒΟςάμ”….
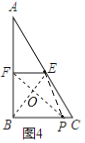
Θ®3Θ©»γΆΦ4Θ§‘ΎRtΓςABC÷–Θ§ABΘΫ8Θ§BCΘΫ6Θ§E «–±±ΏACΒΡ÷–ΒψΘ§F «÷±Ϋ«±ΏABΒΡ÷–ΒψΘ§P «÷±Ϋ«±ΏBC…œ“ΜΕ·ΒψΘ§ ‘ΧΫΨΩΘΚΒ±PCΘΫ_____ ±Θ§ΥΡ±Ώ–ΈBPEF «÷–ΡΗΨΊ–ΈΘΩΘ®÷±Ϋ«»ΐΫ«–Έ÷–Θ§30ΓψΫ«ΥυΕ‘ΒΡ÷±Ϋ«±Ώ «–±±ΏΒΡ“ΜΑκΘ©
ΓΨ¥πΑΗΓΩΘ®1Θ©ΆΦœξΦϊΫβΈωΘ§DΘ®6Θ§4Θ©ΘΜΘ®2Θ©œξΦϊΫβΈωΘΜΘ®3Θ©![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨί÷–ΡΗΨΊ–ΈΒΡΕ®“εΫχΕχΒΟ≥ωΒ±BDΓΈx÷α ±Θ§D‘ΎœΏΕΈAC”“≤ύΦ¥Ω…ΘΜΘ®2Θ©άϊ”Ο’ΐΖΫ–ΈΒΡ–‘÷ ΫαΚœ»ΪΒ»»ΐΫ«–ΈΒΡ≈–Ε®ΖΫΖ®ΒΟ≥ωΓςEACΓ’ΓςGABΘ®SASΘ©Θ§ΫχΕχΒΟ≥ωECΓΆBGΘ§ΒΟ≥ω¥πΑΗΦ¥Ω…ΘΜΘ®3Θ©ΗυΨί÷–ΈΜœΏΒΡ–‘÷ Ω…ΒΟEFΒΡ≥ΛΘ§άϊ”ΟΓΑ÷–ΡΗΨΊ–ΈΓ±ΒΡΕ®“εΫαΚœœύΥΤ»ΐΫ«–ΈΒΡ–‘÷ ”κ≈–Ε®Ω…ΒΟ≥ωBPΒΡ≥ΛΘ§ΫχΕχΩ…ΒΟPCΒΡ≥Λ.
Θ®1Θ©»γΆΦ2Υυ ΨΘΚΒψDΦ¥ΈΣΥυ«σΘ§DΘ®6Θ§4Θ©ΘΜ
Θ®2Θ©»γΆΦ3Θ§
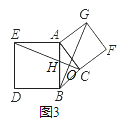
ΓΏΥΡ±Ώ–ΈABDEΦΑACFG «’ΐΖΫ–ΈΘ§
ΓύΓœEABΘΫΓœGACΘΫ90ΓψΘ§AGΘΫACΘ§AEΘΫABΘ§
ΓύΓœEACΘΫΓœEABΘΪΓœBACΘΫΓœGACΘΪΓœBACΘΫΓœGAB
‘ΎΓςEACΚΆΓςGAB÷–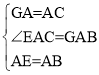
ΓύΓςEACΓ’ΓςGABΘ®SASΘ©Θ§
ΓύΓœABGΘΫΓœAECΘ§
ΓύΓœAECΘΪΓœAHEΘΫΓœABGΘΪΓœBHOΘΫ90ΓψΘ§
ΓύECΓΆBGΘ§
ΓύΥΡ±Ώ–ΈBEGC «÷–ΡΗΨΊ–ΈΘΜ
Θ®3Θ©»γΆΦ4Θ§Ν§Ϋ”BEΘ§ΉςFPΓΆBE”ΎOΘ§ΫΜBC”ΎPΘ§Ν§Ϋ”EPΘ§
ΓύΥΡ±Ώ–ΈBPEF «÷–ΡΗΨΊ–ΈΘ§
ΓΏΓœFPBΘΪΓœBFPΘΫ90ΓψΘ§ΓœEBFΘΪΓœBFPΘΫ90ΓψΘ§
ΓύΓœFPBΘΫΓœFBEΘ§
ΓΏE «–±±ΏACΒΡ÷–ΒψΘ§F «÷±Ϋ«±ΏABΒΡ÷–ΒψΘ§
ΓύEF//BCΘ§BFΘΫ![]() AB=4Θ§EFΘΫ
AB=4Θ§EFΘΫ![]() BC=3Θ§
BC=3Θ§
ΓΏΓœFBC=90ΓψΘ§
ΓύΓœEFB=180Γψ-90Γψ=90ΓψΘ§
ΓύΓœEFB=ΓœFBP=90Γψ
ΓύΓςBFEΓΉΓςPBFΘ§
Γύ![]() Θ§
Θ§
Γύ![]()
ΓύPC=BC-BP=6-![]() =
=![]()
Φ¥Β±P‘ΎBC±Ώ…œΘ§PC=![]() ±Θ§ΥΡ±Ώ–ΈBPEF «÷–ΡΗΨΊ–Έ.
±Θ§ΥΡ±Ώ–ΈBPEF «÷–ΡΗΨΊ–Έ.
Ι ¥πΑΗΈΣΘΚ![]()

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ