题目内容
【题目】如图,抛物线![]() 与
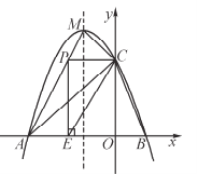
与![]() 轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
轴交于A、B两点,与y轴交于点C(0,3),且此抛物线的顶点坐标为M(-1,4).
(1)求此抛物线的解析式;
(2)设点D为已知抛物线对称轴上的任意一点,当△ACD面积等于6时,求点D的坐标;
(3)点P在线段AM上,当PC与y轴垂直时,过点P作![]() 轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
轴的垂线,垂足为E,将△PCE沿直线CB翻折,使点P的对应点P'与P、E、C处在同一平面内,请求出P'坐标,并判断点P'是否在抛物线上.
【答案】(1) ![]() ;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;M(-1,4);(2)点D的坐标为(-1,-2)或(-1,6).
;(3)点P′不在该抛物线上.
【解析】分析:(1)由抛物线经过的C点坐标以及顶点M的坐标,利用待定系数法即可求出抛物线解析式;
(2)设点D坐标为(﹣1,yD),根据△ACD的面积=6,即可得出关于yD含绝对值符号的一元一次方程,解方程即可得出结论;
(3)作点P关于直线CE的对称点P′,过点P′作PH⊥y轴于H,设P′E交y轴于点N.根据对称的性质即可得出△EON≌△CP′N,从而得出CN=NE,由点A、M的坐标利用待定系数法可求出直线AM的解析式,进而得出点P的坐标.在Rt△P′NC中,由勾股定理可求出CN的值,再由相似三角形的性质以及线段间的关系即可找出点P′的坐标,将其代入抛物线解析式中看等式是否成立,由此即可得出结论.
详解:(1)∵抛物线y=ax2+bx+c经过点C(0,3),顶点为M(﹣1,4),∴ ,解得:
,解得: ,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
,∴所求抛物线的解析式为y=﹣x2﹣2x+3.
(2)依照题意画出图形,如图1所示.
令y=﹣x2﹣2x+3=0,解得:x=﹣3或x=1,故A(﹣3,0),B(1,0),∴OA=OC,△AOC为等腰直角三角形.
设AC交对称轴x=﹣1于F(﹣1,yF),由点A(﹣3,0)、C(0,3)可知直线AC的解析式为y=x+3,∴yF=﹣1+3=2,即F(﹣1,2).
设点D坐标为(﹣1,yD),则S△ADC=![]() DFAO=
DFAO=![]() ×|yD﹣2|×3=6.
×|yD﹣2|×3=6.
解得:yD=﹣2或yD=6,∴点D的坐标为(﹣1,﹣2)或(﹣1,6).
(3)如图2,点P′为点P关于直线CE的对称点,过点P′作PH⊥y轴于H,设P′E交y轴于点N.
在△EON和△CP′N中,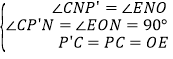 ,∴△EON≌△CP′N(AAS).
,∴△EON≌△CP′N(AAS).
设NC=m,则NE=m.
∵A(﹣3,0)、M(﹣1,4)可知直线AM的解析式为y=2x+6,∴当y=3时,x=﹣![]() ,即点P(﹣
,即点P(﹣![]() ,3),∴P′C=PC=
,3),∴P′C=PC=![]() ,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:
,P′N=3﹣m.在Rt△P′NC中,由勾股定理,得:![]() +(3﹣m)2=m2,解得:m=
+(3﹣m)2=m2,解得:m=![]() .
.
∵S△P′NC=![]() CNP′H=
CNP′H=![]() P′NP′C,∴P′H=
P′NP′C,∴P′H=![]() .
.
由△CHP′∽△CP′N可得:![]() ,∴CH=
,∴CH=![]() =
=![]() ,∴OH=3﹣
,∴OH=3﹣![]() =
=![]() ,∴P′的坐标为(
,∴P′的坐标为(![]() ).
).
将点P′(![]() )代入抛物线解析式,得:y=﹣
)代入抛物线解析式,得:y=﹣![]() ﹣2×
﹣2×![]() +3=
+3=![]() ≠
≠![]() ,∴点P′不在该抛物线上.
,∴点P′不在该抛物线上.