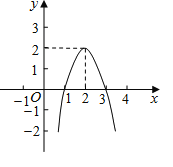题目内容
【题目】如图,平面直角坐标系中,二次函数y=x2-2x-3的部分图象与x轴交于点A,B(A在B的左边),与y轴交于点C,连接BC,D为顶点.
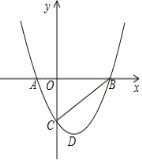
(1)求∠OBC的度数;
(2)在x轴下方的抛物线上是否存在一点Q,使△ABQ的面积等于5?如存在,求Q点的坐标;若不存在,说明理由;
【答案】(1)∠OBC=45;(2)点Q的坐标为(![]() ,
,![]() ), (
), (![]() ,
,![]() )
)
【解析】
(1)由抛物线已知,则可求三角形OBC的各个顶点,易知三角形形状及内角.
(2)因为抛物线已固定,利用设点Q到AB的距离为a以及△ABQ的面积等于5,求出a的值,然后代入二次函数的表达式,即可求出Q点坐标.
(1)∵y=x22x3=(x3)(x+1),
∴当x=0时,y=3,当y=0时,x=1或x=3,
∴点C的坐标为(0,3),点B(3,0),点A(1,0),
∴OC=3,OB=3,∴OB=OC,∴∠OBC=∠OCB,
∵∠BOC=90,∴∠OBC=∠OCB=45,
即∠OBC=45;
(2)在x轴下方的抛物线上存在一点Q,使△ABQ的面积等于5,
∵点B(3,0),点A(1,0),
∴AB=4,
设点Q到AB的距离为a,
∵△ABQ的面积等于5,
∴![]() ,得a=
,得a=![]() ,
,
∵点Q在x轴下方,
∴点Q的纵坐标是![]() ,
,
将y=-![]() 代入y=x2-2x-3,得-
代入y=x2-2x-3,得-![]() =x2-2x-3,
=x2-2x-3,
解得,x=![]()
∴点Q的坐标为(![]() ,
,![]() ) (
) (![]() ,
,![]() )
)

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目