题目内容
(本题满分10分)
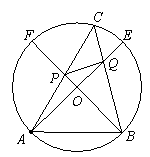
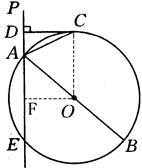
已知:如图直线PA交⊙O于A,E两点,过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C,连接AC,且AC平分∠DAB.
小题1:(1) 试判断DC与⊙O的位置关系?并说明理由.
小题2:(2) 若DC=4,DA=2,求⊙O的直径.
已知:如图直线PA交⊙O于A,E两点,过A点作⊙O的直径AB.PA的垂线DC交⊙O于点C,连接AC,且AC平分∠DAB.
小题1:(1) 试判断DC与⊙O的位置关系?并说明理由.
小题2:(2) 若DC=4,DA=2,求⊙O的直径.

小题1:(1) DC与⊙O相切. ……………………1分
理由:连结OC ∵ AC平分∠DAB
∴∠PAC=∠OAC ……………………2分
又 OC=OA
 ∴ ∠OCA=∠OAC
∴ ∠OCA=∠OAC∴∠PAC=∠OCA
∴ OC∥PA
∴∠PDC=∠OCD ……………………4分
又∵PA⊥DC
∴∠PDC=
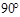
∴∠OCD=
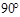
∴OC⊥DC
∴DC切⊙O于C ……………………6分
小题2:(2)作OF⊥AE于F,设⊙O的半径为R
又∵PA⊥DC OC⊥DC
∴四边形OCDF为矩形
∴OF="CD=4 " 且 DF="OC=R "
又 DA=2,∴ AF=DF-AD=R-2……………………8分
在Rt△OAF中,OF2+AF2=OA2
∴ 42+(R-2)2=R2 解得:R=5
∴⊙O的直径:2R="10 " ……………………10分
略

练习册系列答案
相关题目
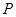 在半径等于3的
在半径等于3的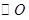 上,则
上,则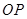 的长( )
的长( )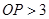
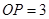
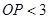
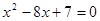 的两个根,且O1O2=7,则⊙O1、⊙O2的位置关系是
的两个根,且O1O2=7,则⊙O1、⊙O2的位置关系是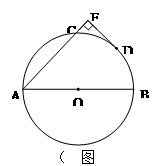
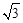 ,
,