Question

【题目】问题提出

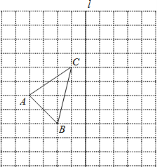
如图①，、是⊙的两条弦， ， 是的中点， ，垂足为．

求证： ．

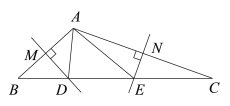
小敏在解答此题时，利用了“补短法”进行证明，她的方法如下：

如图②，延长至，使，连接、、、、．

（请你在下面的空白处完成小敏的证明过程．）

推广运用

如图③，等边内接于⊙， ． 是上一点， ， ，垂足为，则的周长是__________．

拓展研究

如图④，若将“问题提出”中的“是的中点”改成“是的中点”，其余条件不变，“”这一结论还成立吗？若成立，请说明理由；若不成立，写出、、三者之间存在的关系并说明理由．

Answer 1

【答案】

【解析】试题分析：问题提出：首先证明△EAM≌△BAM（SAS），进而得出ME=MC，再利用等腰三角形的性质得出ED=CD，即可得出答案；

推广运用：首先证明△ABF≌ACD（SAS），进而得出AF=AD，以及CD+DE=BE，进而求出DE的长即可得出答案；

拓展研究：连接EA，EF，ED，EB交AC于N，根据已知条件得到∠BEM=∠CEM，根据全等三角形的性质得到CD=ND，∠ECD=∠END，根据等腰三角形的判定得到AN=AB，于是得到结论．

试题解析：问题提出：证明：如图2，延长CA至E，使AE=AB，连接MA、MB、MC、ME、BC，

∵M是的中点，

∴MB=MC，∠MBC=∠MCB，

∵∠MAB=180°-∠MCB，

∵∠EAM=180°-∠CAM=180°-∠MBC，

∴∠EAM=∠BAM，

在△EAM和△BAM中

∵，

∴△EAM≌△BAM（SAS），

∴ME=MC，

又∵MD⊥AC，

∴ED=CD，

∴DC=AD+AE=BA+AD；

推广运用：解：如图3，截取BF=CD，连接AF，AD，CD，

由题意可得：AB=AC，∠ABF=∠ACD，

在△ABF和△ACD中

∵，

∴△ABF≌ACD（SAS），

∴AF=AD，

∵AE⊥BD，

∴FE=DE，则CD+DE=BE，

∵∠ABD=45°，

∴BE==，

则△BDC的周长是1+；

拓展研究：不成立，CD、BA、AD三者之间的关系：AD=BA+CD，

证明：连接EA，EF，ED，EB交AC于N，

∵M是的中点，

∴∠BEM=∠CEM，

在△EDN和△EDC中，

，

∴CD=ND，∠ECD=∠END，

∵∠ECD=∠ABE，∠ENC=∠ANB，

∴∠ANB=∠ABE，

∴AN=AB，

∴AD=AN+∠ND=BA+CD．