Question

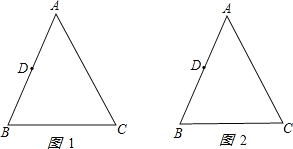
【题目】如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M为曲线部分的最低点，则△ABC的面积是（　　）

A.12B.12C.6D.6

Answer 1

【答案】A

【解析】

由图1可以发现，点P从B运动到A的过程中，y=BP先从0开始增大，到达点C时达到最大，对应图2可知此时y=5，即BC=5；点P从C运动到A的过程中，y=BP先减小，到达BP⊥AC时达到最小，对应图2可知此时BP=4；而后BP又开始增大，到达点d时达到A点时最大y=5，即BA=5，所以△ABC为等腰三角形；作AC边上的高BD =4，由勾股定理可得AD=CD=3，即AC=6，最后用三角形的面积公式解答即可．

解：①当点P在BC上运动时，此时BP不断增大，

∵点P从B向C运动时，BP的最大值为5，

∴BC＝5，

②当点P从C运动到A的过程中，y=BP先减小，到达BP⊥AC时达到最小，

∵M是曲线部分的最低点，

∴BP⊥AC，BP＝4，

∴由勾股定理可得：PC＝3，

∵图象的曲线部分是轴对称图形，图象右端点函数值为5，

∴AB=BC=5，

∴PA＝3，AP＝PC＝3，

∴AC＝6，

∴△ABC的面积为：×4×6＝12，

故选答案为A．