ĢāÄæÄŚČŻ
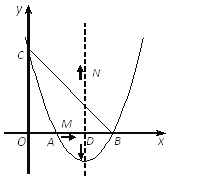
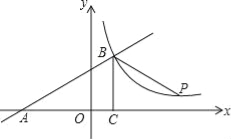
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬Ņ»“ĪŗÆŹż![]() µÄĶ¼ĻóÓė
µÄĶ¼ĻóÓė![]() Öįøŗ°ėÖį½»ÓŚµć
Öįøŗ°ėÖį½»ÓŚµć![]() £¬Óė
£¬Óė![]() ÖįÕż°ėÖį½»ÓŚµć
ÖįÕż°ėÖį½»ÓŚµć![]() £¬µć
£¬µć![]() ĪŖÖ±Ļß
ĪŖÖ±Ļß![]() ÉĻŅ»µć£¬
ÉĻŅ»µć£¬![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ÖįÕż°ėÖįÉĻŅ»µć£¬Į¬½Ó
ÖįÕż°ėÖįÉĻŅ»µć£¬Į¬½Ó![]() £¬
£¬![]() µÄĆ껿ĪŖ48£®
µÄĆ껿ĪŖ48£®
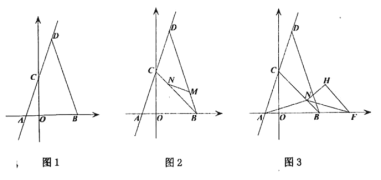
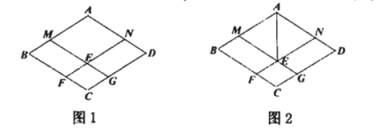
(1)ČēĶ¼1£¬Ēóµć![]() µÄ×ų±ź£»
µÄ×ų±ź£»
(2)ČēĶ¼2£¬µć![]() ·Ö±šŌŚĻ߶Ī
·Ö±šŌŚĻ߶Ī![]() ÉĻ£¬Į¬½Ó
ÉĻ£¬Į¬½Ó![]() £¬µć
£¬µć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬µć
£¬µć![]() µÄŗį×ų±źĪŖ
µÄŗį×ų±źĪŖ![]() £¬Ēó
£¬Ēó![]() Óė
Óė![]() µÄŗÆŹż¹ŲĻµŹ½(²»ŅŖĒ󊓳ö×Ō±äĮæ
µÄŗÆŹż¹ŲĻµŹ½(²»ŅŖĒ󊓳ö×Ō±äĮæ![]() µÄȔֵ·¶Ī§)£»
µÄȔֵ·¶Ī§)£»
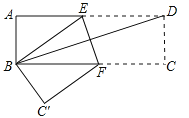
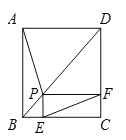
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬ČēĶ¼3£¬Į¬½Ó![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ÖįÕż°ėÖįÉĻµć
ÖįÕż°ėÖįÉĻµć![]() ÓŅ²ąŅ»µć£¬µć
ÓŅ²ąŅ»µć£¬µć![]() ĪŖµŚŅ»ĻóĻŽÄŚŅ»µć£¬
ĪŖµŚŅ»ĻóĻŽÄŚŅ»µć£¬![]() £¬
£¬![]() £¬ŃÓ³¤
£¬ŃÓ³¤![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £¬µć
£¬µć![]() ĪŖ
ĪŖ![]() ÉĻŅ»µć£¬Ö±Ļß
ÉĻŅ»µć£¬Ö±Ļß![]() ¾¹żµć
¾¹żµć![]() ŗĶµć
ŗĶµć![]() £¬¹żµć
£¬¹żµć![]() ×÷
×÷![]() £¬½»Ö±Ļß
£¬½»Ö±Ļß![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬ĒėÄćÅŠ¶ĻĖıߊĪ
£¬ĒėÄćÅŠ¶ĻĖıߊĪ![]() µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄŠĪד£¬²¢ĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©B£Ø6£¬0£©£»£Ø2£©d£½![]() £»£Ø3£©ĖıߊĪ
£»£Ø3£©ĖıߊĪ![]() ŹĒ¾ŲŠĪ£¬ĄķÓɼū½āĪö
ŹĒ¾ŲŠĪ£¬ĄķÓɼū½āĪö
”¾½āĪö”æ
£Ø1£©×÷DL”ĶyÖį“¹×ćĪŖLµć£¬DI”ĶAB“¹×ćĪŖI£¬Ö¤Ć÷”÷DLC”Õ”÷AOC£¬ĒóµĆD£Ø2£¬12£©£¬ŌŁÓÉS”÷ABD£½![]() ABDI£½48£¬ĒóµĆOB£½ABAO£½82£½6£¬¼“æÉĒóB×ų±ź£»
ABDI£½48£¬ĒóµĆOB£½ABAO£½82£½6£¬¼“æÉĒóB×ų±ź£»
£Ø2£©Éč”ĻMNB£½”ĻMBN£½¦Į£¬×÷NK”ĶxÖį“¹×ćĪŖK£¬MQ”ĶAB“¹×ćĪŖQ£¬MP”ĶNK£¬“¹×ćĪŖP£»Ö¤Ć÷ĖıߊĪMPKQĪŖ¾ŲŠĪ£¬ŌŁÖ¤Ć÷”÷MNP”Õ”÷MQB£¬Ēó³öBDµÄ½āĪöŹ½ĪŖy£½3x£«18£¬MQ£½d£¬°Ńy£½d“śČėy£½3x£«18µĆd£½3x£«18£¬±ķ“ļ³öOQµÄÖµ£¬ŌŁÓÉOQ£½OK£«KQ£½t£«d£¬æɵĆd£½![]() £»
£»
£Ø3£©×÷NW”ĶAB“¹×ćĪŖW£¬Ö¤Ć÷”÷ANW”Õ”÷CAO£¬øł¾Ż±ßµÄ¹ŲĻµĒóµĆN£Ø4£¬2£©£»ŃÓ³¤NWµ½Y£¬Ź¹NW£½WY£¬×÷NS”ĶYF£¬ŌŁÖ¤Ć÷”÷FHN”Õ”÷FSN£¬æɵĆSF£½FH=![]() £¬NY£½2£«2£½4£»ÉčYS£½a£¬FY£½FN£½a£«
£¬NY£½2£«2£½4£»ÉčYS£½a£¬FY£½FN£½a£«![]() £¬ŌŚRt”÷NYSŗĶRt”÷FNSÖŠĄūÓĆ¹“¹É¶ØĄķĒóµĆFN£»ŌŚRt”÷NWFÖŠ£¬ĄūÓĆ¹“¹É¶ØĄķĒó³öWF£½6£¬µĆµ½F£Ø10£¬0£©£»ÉčGF½»yÖįÓŚµćT£¬ÉčFNµÄ½āĪöŹ½ĪŖy£½px£«q£Øp”Ł0£©°ŃF£Ø10£¬0£©N£Ø4£¬2£©“śČė¼“æÉĒó³öÖ±ĻßFNµÄ½āĪöŹ½£¬ĮŖĮ¢·½³Ģ×éµĆµ½Gµć×ų±ź£»°ŃGµć“śČėµĆµ½y£½
£¬ŌŚRt”÷NYSŗĶRt”÷FNSÖŠĄūÓĆ¹“¹É¶ØĄķĒóµĆFN£»ŌŚRt”÷NWFÖŠ£¬ĄūÓĆ¹“¹É¶ØĄķĒó³öWF£½6£¬µĆµ½F£Ø10£¬0£©£»ÉčGF½»yÖįÓŚµćT£¬ÉčFNµÄ½āĪöŹ½ĪŖy£½px£«q£Øp”Ł0£©°ŃF£Ø10£¬0£©N£Ø4£¬2£©“śČė¼“æÉĒó³öÖ±ĻßFNµÄ½āĪöŹ½£¬ĮŖĮ¢·½³Ģ×éµĆµ½Gµć×ų±ź£»°ŃGµć“śČėµĆµ½y£½![]() x+3£¬æÉÖŖR£Ø4£¬0£©£¬Ö¤Ć÷”÷GRA”Õ”÷EFR£¬æɵĆĖıߊĪAGFEĪŖĘ½ŠŠĖıߊĪ£¬ŌŁÓÉ”ĻAGF£½180”ć”ĻCGF£½90”ć£¬æÉÖ¤Ć÷Ę½ŠŠĖıߊĪAGFEĪŖ¾ŲŠĪ£®
x+3£¬æÉÖŖR£Ø4£¬0£©£¬Ö¤Ć÷”÷GRA”Õ”÷EFR£¬æɵĆĖıߊĪAGFEĪŖĘ½ŠŠĖıߊĪ£¬ŌŁÓÉ”ĻAGF£½180”ć”ĻCGF£½90”ć£¬æÉÖ¤Ć÷Ę½ŠŠĖıߊĪAGFEĪŖ¾ŲŠĪ£®
½ā£ŗ£Ø1£©Įīx£½0£¬y£½6£¬Įīy£½0£¬x£½2£¬
”ąA£Ø2£¬0£©£¬B£Ø0£¬6£©£¬
”ąAO£½2£¬CO£½6£¬
×÷DL”ĶyÖį“¹×ćĪŖLµć£¬DI”ĶAB“¹×ćĪŖI£¬
”ą”ĻDLO£½”ĻCOA£½90”ć£¬”ĻDCL£½”ĻACO£¬DC£½AC£¬
”ą”÷DLC”Õ”÷AOC£ØAAS£©£¬
”ąDL£½AO£½2£¬
”ąDµÄŗį×ų±źĪŖ2£¬
°Ńx£½2“śČėy£½3x£«6µĆy£½12£¬
”ąD£Ø2£¬12£©£¬
”ąDI£½12£¬
”ßS”÷ABD£½![]() ABDI£½48£¬
ABDI£½48£¬
”ąAB£½8£»
”ßOB£½ABAO£½82£½6£¬
”ąB£Ø6£¬0£©£»

£Ø2£©”ßOC£½OB£½6£¬
”ą”ĻOCB£½”ĻCBO£½45”ć£¬
”ßMN£½MB£¬
”ąÉč”ĻMNB£½”ĻMBN£½¦Į£¬
×÷NK”ĶxÖį“¹×ćĪŖK£¬MQ”ĶAB“¹×ćĪŖQ£¬MP”ĶNK£¬“¹×ćĪŖP£»
”ą”ĻNKB£½”ĻMQK£½”ĻMPK£½90”ć£¬
”ąĖıߊĪMPKQĪŖ¾ŲŠĪ£¬
”ąNK”ĪCO£¬MQ£½PK£»
”ß”ĻKNB£½90”ć45”ć£½45”ć£¬
”ą”ĻMNK£½45”ć£«¦Į£¬”ĻMBQ£½45”ć£«¦Į£¬
”ą”ĻMNK£½”ĻMBQ£¬
”ßMN£½MB£¬”ĻNPM£½”ĻMQB£½90”ć£¬
”ą”÷MNP”Õ”÷MQB£ØAAS£©£¬
”ąMP£½MQ£»
”ßB£Ø6£¬0£©£¬D£Ø2£¬12£©£¬
”ąÉčBDµÄ½āĪöŹ½ĪŖy£½kx£«b£Øk”Ł0£©£¬
”ą![]() £¬½āµĆ£ŗk=-3£¬b=18£¬
£¬½āµĆ£ŗk=-3£¬b=18£¬
”ąBDµÄ½āĪöŹ½ĪŖy£½3x£«18£¬
”ßµćMµÄׯ×ų±źĪŖd£¬
”ąMQ=MP£½d£¬°Ńy£½d“śČėy£½3x£«18µĆd£½3x£«18£¬
½āµĆx£½![]() £¬
£¬
”ąOQ£½![]() £»
£»
”ßNµÄŗį×ų±źĪŖt£¬
”ąOK£½t£¬
”ąOQ£½OK£«KQ£½t£«d£¬
”ą![]() £½t£«d£¬
£½t£«d£¬
”ąd£½![]() £»
£»
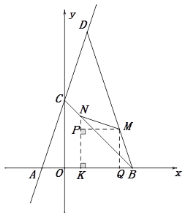
£Ø3£©×÷NW”ĶAB“¹×ćĪŖW£¬
”ą”ĻNWO£½90”ć£¬
”ß”ĻACN£½45”ć£«”ĻACO£¬”ĻANC£½45”ć£«”ĻNAO£¬
”ß”ĻACO£½”ĻNAO£¬
”ą”ĻACN£½”ĻANC£¬
”ąAC£½AN£¬
Ó֔ߔĻACO£½”ĻNAO£¬”ĻAOC£½”ĻNOW£½90”ć£¬
”ą”÷ANW”Õ”÷CAO£ØAAS£©£¬
”ąAO£½NW£½2£¬
”ąWB£½NW£½2£¬
”ąOW£½OBWB£½62£½4£¬
”ąN£Ø4£¬2£©£»
ŃÓ³¤NWµ½Y£¬Ź¹NW£½WY£¬
”ą”÷NFW”Õ”÷YFW£ØSAS£©
”ąNF£½YF£¬”ĻNFW£½”ĻYFW£¬
Ó֔ߔĻHFN£½2”ĻNFO£¬
”ą”ĻHFN£½”ĻYFN£¬
×÷NS”ĶYF£¬
”ß”ĻFH”ĶNH£¬
”ą”ĻH
”ßFN£½FN£¬
”ą”÷FHN”Õ”÷FSN£ØAAS£©£¬
”ąSF£½FH£½![]() £¬NY£½2£«2£½4£¬
£¬NY£½2£«2£½4£¬
ÉčYS£½a£¬FY£½FN£½a£«![]() £¬
£¬
ŌŚRt”÷NYSŗĶRt”÷FNSÖŠ£ŗNS2£½NY2YS2£»NS2£½FN2FS2£»NY2YS2£½FN2FS2£¬
”ą42a2£½(a£«![]() )2-(
)2-(![]() )2£¬
)2£¬
½āµĆa£½![]()
”ąFN£½![]() £»
£»
ŌŚRt”÷NWFÖŠWF£½![]() £¬
£¬
”ąFO£½OW£«WF£½4£«6£½10£¬
”ąF£Ø10£¬0£©£¬
”ąAW£½AO£«OW£½2£«4£½6£¬
”ąAW£½FW£¬
”ßNW”ĶAF£¬
”ąNA£½NF£¬
”ą”ĻNFA£½”ĻNAF£¬
”ß”ĻACO£½”ĻNAO£¬
”ą”ĻNFA£½”ĻACO£¬
ÉčGF½»yÖįÓŚµćT£¬”ĻCTF£½”ĻACO£«”ĻCGF£½”ĻCOF£«”ĻGFO£¬
”ą”ĻCGF£½”ĻCOF£½90”ć£¬
ÉčFNµÄ½āĪöŹ½ĪŖy£½px£«q£Øp”Ł0£©£¬°ŃF£Ø10£¬0£©N£Ø4£¬2£©“śČėy£½px£«q
µĆ![]() £¬½āµĆ
£¬½āµĆ £¬
£¬
”ą![]() £¬
£¬
”ąĮŖĮ¢ £¬½āµĆ£ŗ
£¬½āµĆ£ŗ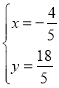 £¬
£¬
”ą![]() £¬
£¬
°ŃGµć“śČėy£½mx£«3£¬µĆ![]() £¬µĆm£½
£¬µĆm£½![]() £¬
£¬
”ąy£½![]() x£«3£¬
x£«3£¬
Įīy£½0µĆ0£½![]() x£«3£¬x£½4£¬
x£«3£¬x£½4£¬
”ąR£Ø4£¬0£©£¬
”ąAR£½AO£«OR£½2£«4£½6£¬RF£½OFOR£½104£½6£¬
”ąAR£½RF£¬
”ßFE”ĪAC£¬
”ą”ĻFEG£½”ĻAGE£¬”ĻGAF£½”ĻEFA£¬
”ą”÷GRA”Õ”÷EFR£ØAAS£©£¬
”ąEF£½AG£¬
”ąĖıߊĪAGFEĪŖĘ½ŠŠĖıߊĪ£¬
”ß”ĻAGF£½180”ć”ĻCGF£½180”ć90”ć£½90”ć£¬
”ąĘ½ŠŠĖıߊĪAGFEĪŖ¾ŲŠĪ£®