题目内容
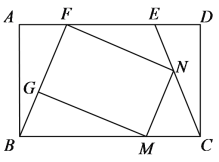
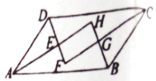
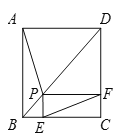
【题目】如图,P是正方形ABCD的对角线BD上一点,PE⊥BC于E,PF⊥CD于F,连接EF,给出下列三个结论:①AP=EF;②△APD一定是等腰三角形;③∠PFE=∠BAP.其中正确结论的序号是( )
A.①②B.①③C.②③D.①②③
【答案】B
【解析】
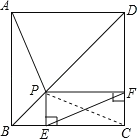
连接PC,根据正方形的对角线平分一组对角可得∠ABP=∠CBP=45°,然后利用“边角边”证明△ABP和△CBP全等,根据全等三角形对应边相等可得AP=PC,对应角相等可得∠BAP=∠BCP,再根据矩形的对角线相等可得EF=PC,于是得到结论.
解:如图,连接PC,在正方形ABCD中,∠ABP=∠CBP=45°,AB=CB,
∵在△ABP和△CBP中,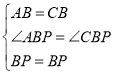 ,
,
∴△ABP≌△CBP(SAS),
∴AP=PC,∠BAP=∠BCP,
又∵PE⊥BC,PF⊥CD,
∴四边形PECF是矩形,
∴PC=EF,∠BCP=∠PFE,
∴AP=EF,∠PFE=∠BAP,故①③正确;
只有点P为BD的中点或PD=AD时,△APD是等腰三角形,故②错误;
故选:B.

练习册系列答案
相关题目
【题目】某学校八年级开展英语拼写大赛,一班和二班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩如图所示:
(1)根据图示填写下表
班级 | 中位数(分) | 众数(分) | 平均数(分) |
一班 | 85 | ||
二班 | 100 | 85 |
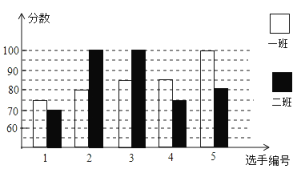
(2)结合两班复赛成绩的平均数和中位数,分析哪个班级的复赛成绩比较好?
(3)已知一班的复赛成绩的方差是70,请求出二班复试成绩的方差,并说明哪个班成绩比较稳定?